15. Apr 2019
Lesedauer 14 Min.
CUDA mit Python
Vollgas mit der GPU, Teil 2
Die Python-Bibliothek numba vereinfacht das Programmieren von GPU-Berechnungen.
dotnetpro
Im ersten Teil dieser Serie [1] wurde gezeigt, wie mit C/C++ direkt auf die CUDA-Bibliotheken zugegriffen wird. Allerdings ist es nicht jedermanns Sache, eine Kernel-Funktion in der Sprache C zu programmieren. Auf der Suche nach einer einfacheren Möglichkeit, Code auf einer Grafikkarte (GPU) auszuführen, findet man die Python-Bibliothek numba. Die ist schnell installiert, sofern bereits eine Python-Umgebung vorhanden ist. Zuerst muss das aktuelle CUDA-SDK installiert werden [2], dann folgt die Zusatz-Bibliothek installieren mit:
pip <span class="hljs-keyword">install</span> numba
Die Installation lässt sich leicht überprüfen, indem Sie folgenden Code in der Python-Umgebung ausführen:
<span class="hljs-keyword">import</span> numba
numba.__version__
Bitte beachten Sie, dass vor und nach dem Befehl version je zwei Unterstriche einzugeben sind. Damit die numba-Bibliothek funktioniert, muss die im Rechner vorhandene Grafikkarte mindestens die CUDA Compute Capabilities 2.0 unterstützen – mehr dazu finden Sie in [1]. Mit numba werden die Main-Funktion und die Kernel-Funktion, welche auf der Grafikkarte ausgeführt werden soll, ganz normal in Python programmiert. Das vereinfacht den gesamten Entwicklungsprozess, da sich mit Python deutlich einfacher programmieren lässt als mit dem C-Dialekt von Nvidia. Zwar gibt es für den GPU-Code in Python einige Einschränkungen, die sind aber zunächst nicht entscheidend.
Ein einfaches Beispiel
Im ersten Beispiel soll auf der GPU ein Array mit Zahlen mit der Zahl 2 multipliziert werden. Dabei sollen zunächst einmal alle Automatismen der Bibliothek zum Einsatz kommen. Schon in [1] wurde beschrieben, dass der generelle Ablauf einer Berechnung auf der GPU der folgende ist:- Speicher auf der GPU allokieren,
- Daten auf die GPU kopieren,
- Kernel auf der GPU ausführen,
- Ergebnisse von der GPU in den Host zurückkopieren,
- Speicher auf der GPU freigeben.
Listing 1: Array-Elemente mit 2 multiplizieren
import numpy as np <br/>from numba import cuda <br/><br/># Die Python-Funktion für die Grafikkarte<br/>@cuda.jit <br/>def mult<span class="hljs-emphasis">_by_</span>two(arr): <br/> # Ermittlung des Array-Index <br/> tx = cuda.threadIdx.x <br/> ty = cuda.blockIdx.x <br/> bw = cuda.blockDim.x <br/> pos = tx + ty <span class="hljs-bullet">* bw </span><br/><span class="hljs-bullet"> </span><br/><span class="hljs-bullet"> # Abfrage, ob Index gültig ist </span><br/><span class="hljs-bullet"> if pos &lt; arr.size: </span><br/><span class="hljs-bullet"> arr[pos] *</span>= 2 <br/> # Debugging <br/> #print(pos, arr[<span class="hljs-string">pos</span>]) <br/> <br/># <span class="hljs-strong">*****</span> Main Programm <span class="hljs-strong">*****</span> <br/>a = np.array([<span class="hljs-string">0, 1, 2, 3, 4, 5</span>]) <br/><br/># GPU-Funktion starten <br/>mult<span class="hljs-emphasis">_by_</span>two[<span class="hljs-string">1, 6</span>](<span class="hljs-link">a</span>) <br/><br/># Ergebnisausgabe <br/>print(a)
In den ersten Zeilen des Beispielprogramms werden die Bibliotheken numpy und numba importiert. Danach wird die Funktion programmiert, die auf der GPU ausgeführt werden soll. Dieser Code bekommt eine spezielle Auszeichnung:
@cuda.jit. Diese sorgt dafür, dass die darauf folgende Funktion so übersetzt wird, dass sie auf der Grafikkarte läuft. Es folgt die Funktion mult_by_two, welche einen Parameter arr hat. Das Array arr enthält die Daten, die im Kernel verarbeitet werden sollen. Die Kopieraktion vom Host-Speicher (CPU) in den Grafikspeicher (GPU) wird hier implizit ausgeführt. Später stellen wir noch Funktionen vor, mit denen der Softwareentwickler den Kopierprozess kontrollieren kann. Aktuell ist weiter nichts zu tun, um die Daten auf der GPU zur Verfügung zu stellen.Im nächsten Programmteil gilt es, aus den CUDA-Variablen threadIdx.x, blockIdx.x und blockDim.x die Nummer des jeweiligen CUDA-Threads zu bestimmen. Diese Nummer ist dann der Array-Index pos für die Verarbeitung der Arrays arr. Die Bedeutung der einzelnen Indices wurde in [1] erklärt. Beim Aufruf der Kernel-Funktion ist anzugeben, wie viele Threads und Blöcke bei der Berechnung benutzt werden sollen.Da der Array-Index pos über die Anzahl der im Kernel-Aufruf angegebenen Threads und Blöcke berechnet wird, sollten Sie als Nächstes unbedingt prüfen, ob dieser Index innerhalb des Arrays arr liegt. Danach kann das jeweilige Array-Element mit der Zahl 2 multipliziert werden.In der Main-Funktion wird zunächst ein numpy-Array a erzeugt und direkt mit Daten gefüllt. Danach wird die Kernel-Funktion aufgerufen. In den eckigen Klammern werden die Parameter 1 und 6 übergeben, das heißt, es wird in einem Block mit sechs Threads auf der GPU gerechnet. Hier wurden diese Parameter statisch angegeben. Normalerweise erfolgt ihre Berechnung je nach Problem und Array-Größe vor dem Kernel-Aufruf. Eine andere Variante wäre die Benutzung von zwei Blöcken mit jeweils drei Threads:
@cuda.jit. Diese sorgt dafür, dass die darauf folgende Funktion so übersetzt wird, dass sie auf der Grafikkarte läuft. Es folgt die Funktion mult_by_two, welche einen Parameter arr hat. Das Array arr enthält die Daten, die im Kernel verarbeitet werden sollen. Die Kopieraktion vom Host-Speicher (CPU) in den Grafikspeicher (GPU) wird hier implizit ausgeführt. Später stellen wir noch Funktionen vor, mit denen der Softwareentwickler den Kopierprozess kontrollieren kann. Aktuell ist weiter nichts zu tun, um die Daten auf der GPU zur Verfügung zu stellen.Im nächsten Programmteil gilt es, aus den CUDA-Variablen threadIdx.x, blockIdx.x und blockDim.x die Nummer des jeweiligen CUDA-Threads zu bestimmen. Diese Nummer ist dann der Array-Index pos für die Verarbeitung der Arrays arr. Die Bedeutung der einzelnen Indices wurde in [1] erklärt. Beim Aufruf der Kernel-Funktion ist anzugeben, wie viele Threads und Blöcke bei der Berechnung benutzt werden sollen.Da der Array-Index pos über die Anzahl der im Kernel-Aufruf angegebenen Threads und Blöcke berechnet wird, sollten Sie als Nächstes unbedingt prüfen, ob dieser Index innerhalb des Arrays arr liegt. Danach kann das jeweilige Array-Element mit der Zahl 2 multipliziert werden.In der Main-Funktion wird zunächst ein numpy-Array a erzeugt und direkt mit Daten gefüllt. Danach wird die Kernel-Funktion aufgerufen. In den eckigen Klammern werden die Parameter 1 und 6 übergeben, das heißt, es wird in einem Block mit sechs Threads auf der GPU gerechnet. Hier wurden diese Parameter statisch angegeben. Normalerweise erfolgt ihre Berechnung je nach Problem und Array-Größe vor dem Kernel-Aufruf. Eine andere Variante wäre die Benutzung von zwei Blöcken mit jeweils drei Threads:
mult<span class="hljs-emphasis">_by_</span>two[<span class="hljs-string">2, 3</span>](<span class="hljs-link">a</span>)
In den runden Klammern werden die Daten an den Kernel übergeben. Hier findet implizit der Kopiervorgang für das Array a in den Speicher der GPU statt. Am Ende des Beispiels erfolgt die Ausgabe des Array a. Hierbei sind die Daten aus dem GPU-Speicher wieder zurück in den Host-Speicher zu kopieren. Das Programm lässt sich nun aus einer Python-IDE heraus (zum Beispiel Spyder) oder direkt auf der Kommandozeile ausführen:
python Listing1.py
# Als Ergebnis erhalten Sie folgendes Array:
# [ <span class="hljs-number">0</span> <span class="hljs-number">2</span> <span class="hljs-number">4</span> <span class="hljs-number">6</span> <span class="hljs-number">8</span> <span class="hljs-number">10</span>]
Im if-Statement des GPU-Codes ist noch eine Kommentarzeile vorhanden, die eine interessante Möglichkeit zum einfachen Debuggen des GPU-Codes aufzeigt:
<span class="hljs-keyword">print</span> (<span class="hljs-keyword">pos</span>, arr[<span class="hljs-keyword">pos</span>])
Aktivieren Sie diese Codezeile, können Sie auf einfache Weise verschiedene Zwischenergebnisse mit print auf der Python-Konsole ausgeben.Obwohl der Code in Listing 1 sehr einfach und übersichtlich ist, wird er trotzdem langsamer sein als eine direkte Multiplikation im numpy-Array. Hier spielen verschiedene Faktoren eine Rolle: Die Bibliothek numba muss geladen und initialisiert werden, der Kernel-Code muss für die GPU übersetzt und der Kernel muss gestartet werden, die Daten müssen in die GPU übertragen und das Ergebnis-Array wieder zurückkopiert werden. Diese Operationen dauern relativ lange. Auch hier gilt also: Die Aufgabenstellung sollte viele zu berechnende Daten aufweisen und nach Möglichkeit sollten die Daten mehrfach benutzt werden.Der Code in Listing 1 lässt sich noch weiter vereinfachen. Der Array-Index pos lässt sich nämlich direkt mit der numba-Funktion grid berechnen. Die Vereinfachung in der Kernel-Funktion zeigt Listing 2. Der Rest des Codes entspricht dem aus Listing 1.Da die Thread- und Block-Variablen bis zu dreidimensional sein können, muss beim Aufruf der grid-Funktion als Parameter die gewünschte Dimension (hier: 1) für die Indexberechnung angegeben werden.
Listing 2: Vereinfachte Index-Berechnung
# Die folgende Python-Funktion soll <br/># auf der Grafikkarte laufen <br/>@cuda.jit <br/>def mult_by_two(arr): <br/> # Ermitteln des Array-Index <br/> pos = cuda.grid(<span class="hljs-number">1</span>) <br/> <br/> # Abfrage, ob der Index gültig ist <br/> <span class="hljs-keyword">if</span> pos &lt; arr.size: <br/> arr[pos] *= <span class="hljs-number">2</span>
Wie in den Beispielen zu sehen war, kann ein GPU-Kernel kein Ergebnis zurückgeben (return). Außerdem muss beim Aufruf eines Kernels die Block- und Thread-Konfiguration in eckigen Klammern angegeben werden. Der Aufruf eines Kernels erfolgt synchron. Das heißt, die Kernel-Funktion kehrt erst dann zurück, wenn sie vollständig ausgeführt wurde. Ein Synchronisierungsmechanismus ist nicht erforderlich.Wenn mit beliebig großen Arrays gerechnet werden soll, ist die benötigte Thread- und Blockanzahl zu berechnen. Legen Sie zunächst fest, wie viele Threads in einem Block verarbeitet werden sollen, dann können Sie die Anzahl der benötigten Blöcke für das Array arr wie folgt ermitteln:
threadsPerBlock = 32
blocksPerGrid =
(arr.size + (threadsPerBlock – 1)) // threadsPerBlock
# Kernel-Aufruf
mult<span class="hljs-emphasis">_by_</span>two[<span class="hljs-string">blocksPerGrid, threadsPerBlock</span>](<span class="hljs-link">a</span>)
Die Division mit // liefert einen Integer-Wert zurück. In allen Berechnungen auf der GPU ist unbedingt darauf zu achten, dass keine illegalen Array-Indices in die Berechnung einbezogen werden. Bei einer Array-Größe von 10.000 und 32 Threads pro Block erhält man 313 Blöcke. Der 313te Block verarbeitet aber die Array-Indices von 9.984 bis 10.015. Das bedeutet, dass die Indices von 10.000 bis 10.015 ignoriert werden müssen. Dies geschieht mit der if-Abfrage vor dem eigentlichen Array-Zugriff.
Mehrdimensionale Arrays
In vielen Rechenalgorithmen kommen zwei- oder höherdimensionale Arrays vor. Solche Arrays lassen sich mit numba und CUDA sehr einfach verarbeiten, da die Variablen für die Threads pro Block und Blocks pro Grid bis zu dreidimensional sein dürfen. Die Vorgehensweise für ein zweidimensionales Array zeigt Listing 3.Listing 3: Zweidimensionale Arrays
import numpy as np <br/>from numba import cuda <br/><br/>@cuda.jit <br/>def flip<span class="hljs-emphasis">_array(arr): </span><br/><span class="hljs-emphasis"> # 2-dim. Index in x und y </span><br/><span class="hljs-emphasis"> x, y = cuda.grid(2) </span><br/><span class="hljs-emphasis"> </span><br/><span class="hljs-emphasis"> # Überprüfung beider Indices x und y </span><br/><span class="hljs-emphasis"> if x &lt; arr.shape[0] and </span><br/><span class="hljs-emphasis"> y &lt; arr.shape[1] and y &lt; x: </span><br/><span class="hljs-emphasis"> arr_</span>help = arr[<span class="hljs-string">x, y</span>] <br/> arr[<span class="hljs-string">x, y</span>] = arr[<span class="hljs-string">y, x</span>] <br/> arr[<span class="hljs-string">y, x</span>] = arr<span class="hljs-emphasis">_help </span><br/><span class="hljs-emphasis"> </span><br/><span class="hljs-emphasis"># ******* Main Programm ******* </span><br/><span class="hljs-emphasis">a = np.zeros(10000) </span><br/><span class="hljs-emphasis">for i in range(10000): </span><br/><span class="hljs-emphasis"> a[i] = i </span><br/><span class="hljs-emphasis"> </span><br/><span class="hljs-emphasis">a.shape = (100, 100) </span><br/><br/><span class="hljs-emphasis"># Test-Ausgabe einiger Elemente </span><br/><span class="hljs-emphasis">print(a[2, 0], a[0, 3], a[1, 2], a[10, 3], a[5, 7]) </span><br/><br/><span class="hljs-emphasis"># Variablen als Tupel mit zwei Werten </span><br/><span class="hljs-emphasis"># für zwei Dimensionen </span><br/><span class="hljs-emphasis">threadsPerBlock = (10, 10) </span><br/><span class="hljs-emphasis">blocksPerGrid = (10, 10) </span><br/><span class="hljs-emphasis">flip_</span>array[<span class="hljs-string">blocksPerGrid, threadsPerBlock</span>](<span class="hljs-link">a</span>) <br/><br/># Test-Ausgabe mit vertauschten Indices <br/># Es müssen die gleichen Zahlen erscheinen <br/>print(a[0, 2], a[3, 0], a[2, 1], a[3, 10], a[7, 5])
Im Beispiel sollen die Elemente in einem quadratischen Array vertauscht werden, man sagt auch: Die Matrix soll gestürzt werden. Hier ein einfaches Beispiel. Das Ausgangs-Array enthält folgende Elemente:
[[ <span class="hljs-number">1</span>, <span class="hljs-number">2</span>, <span class="hljs-number">3</span>],
[ <span class="hljs-number">4</span>, <span class="hljs-number">5</span>, <span class="hljs-number">6</span>],
[ <span class="hljs-number">7</span>, <span class="hljs-number">8</span>, <span class="hljs-number">9</span>]]
Die gestürzte Matrix erhält man, wenn man beim Zugriff auf die Elemente die beiden Indices einfach vertauscht. Man kann die Datenelemente jedoch auch tatsächlich austauschen, indem man zum Beispiel das Element a[3, 1] in das Element a[1, 3] kopiert. Man erhält folgendes Ergebnis:
[[ <span class="hljs-number">1</span>, <span class="hljs-number">4</span>, <span class="hljs-number">7</span>],
[ <span class="hljs-number">2</span>, <span class="hljs-number">5</span>, <span class="hljs-number">8</span>],
[ <span class="hljs-number">3</span>, <span class="hljs-number">6</span>, <span class="hljs-number">9</span>]]
In der GPU-Kernel-Funktion flip_array werden zunächst die beiden erforderlichen Array-Indices ermittelt. Der Aufruf von grid(2) liefert nun zwei Variablen, x und y, welche den Index in der waagerechten und den Index in der senkrechten Richtung für das Array enthalten.Mit dem if-Befehl werden zwei wichtige Bedingungen geprüft. Zuerst wird ermittelt, ob die beiden Indices im jeweiligen Bereich der Array-Größe liegen. Hier kommt die shape-Funktion zum Einsatz, um die jeweils richtige Größe des Arrays in X- oder Y-Richtung zu erhalten. Die letzte Bedingung im if-Befehl sorgt dafür, dass nur eine Seite der Diagonale des Arrays durchlaufen wird, denn sonst würde man die gerade vertauschten Array-Elemente wieder zurücktauschen. Nun kann das Vertauschen der Werte stattfinden. Man muss sich darüber im Klaren sein, dass dieses Programm nicht sonderlich effizient ist, da etwa die Hälfte aller Threads aufgrund der if-Bedingungen gar nicht benutzt werden.Im Hauptprogramm in Listing 3 wird ein numpy-Array der Größe 10.000 erzeugt und mit den Zahlen von 1 bis 10.000 gefüllt. Danach wird das Array auf die Größe 100 x 100 umkonfiguriert. In diesem Fall wird die Variable threadsPerBlock mit dem Tupel (10, 10) initialisiert. In jedem Block werden also 100 Threads benutzt. Die CUDA-Variable blocksPerGrid wird ebenfalls mit dem Tupel (10, 10) initialisiert. Werden nun im Kernel die entsprechenden Indices berechnet, sind zwei Aktionen durchzuführen: Einmal wird mit den CUDA-Variablen threadIdx.x, blockIdx.x und blockDim.x der Array-Index x ermittelt und mit den Variablen threadIdx.y,blockIdx.y und blockDim.y wird der Array-Index y bestimmt.Die Kernel-Funktion wird nun mit den beiden Tupeln in eckigen Klammern und dem Array als Parameter in runden Klammern gestartet.In das Programm wurde noch die Ausgabe einiger Array-Elemente vor und nach dem Kernel eingebaut, um die korrekte Ausführung zu prüfen. Beide Ausgaben liefern das gleiche Ergebnis, da die beiden Indices in den print-Befehlen vertauscht wurden.
Reduktionen
Reduktionen sind mit der CUDA-Bibliothek nicht ganz so einfach zu realisieren. Worum geht es bei einer Reduktion (oder auch Aggregation)? Es sollen mehrere Zahlen in einer Variablen zusammengefasst werden. Und genau hier liegt auch das Problem. Wird die Zusammenfassung in mehreren Threads ausgeführt, dann greifen diese Threads alle gleichzeitig auf die Reduktionsvariable zu, und das ergibt ein erstklassiges Data Race mit falschem Rechenergebnis. Der folgende Codeschnipsel zeigt eine typische Reduktionsoperation:
summe = <span class="hljs-number">0.0</span>
<span class="hljs-function"><span class="hljs-keyword">for</span> i <span class="hljs-keyword">in</span> <span class="hljs-title">range</span>(<span class="hljs-params"><span class="hljs-number">10</span></span>): </span>
<span class="hljs-function"> summe +</span>= a[i] <span class="hljs-meta"># Reduktion </span>
Die Datenwerte aus dem Array a werden in der Variablen summe zusammengezählt. Solche Reduktionen kommen in Programmen sehr häufig vor. Darum gibt es in numba die Kennzeichnung @cuda.reduce, die solche Summierungen ermöglicht. Listing 4 zeigt ein einfaches Beispiel, in dem die Zahlen (von 0 bis 100) im Array arr addiert werden. Dazu wird eine Funktion sum_reduce definiert, welche die Summe zweier Zahlen zurückgibt. Durch die Kennzeichnung der Funktion mit @cuda.reduce wird diese Addition Schritt für Schritt für alle Array-Elemente aufgerufen.
Listing 4: Eine einfache Reduktion
<span class="hljs-keyword">import</span> numpy <br/>from numba <span class="hljs-keyword">import</span> cuda <br/><br/># Funktion für die Reduktion <br/>@cuda.reduce <br/>def sum_reduce(a, b): <br/> #print (a, b) <br/> return a + b <br/><br/># ******* Main Programm ****** <br/>arr = (numpy.arange(100, dtype=numpy.float64)) <br/>#print (arr) <br/><br/>result_1 = arr.sum() # numpy Reduktion <br/>result_2 = sum_reduce(arr) # Cuda Reduktion <br/><br/># Ergebnisse müssen gleich sein <br/>print(result_1) <br/>print(result_2)
Den Additionsvorgang können Sie sehr schön mitverfolgen, wenn Sie die beiden print-Befehle, die als Kommentare im Code stehen, aktivieren.
Die Speicherverwaltung
In den bisherigen Beispielen wurden die erforderlichen Daten einfach als Array-Parameter an die Kernel-Funktion übergeben. In diesen Fällen übernehmen Funktionen der numba-Bibliothek die Allokation des Speichers und das Kopieren der Daten in den GPU-Speicher. Der Kopierprozess lässt sich jedoch auch kontrolliert ausführen. Die beiden wichtigsten Funktionen in diesem Zusammenhang sind cuda.to_device(...) und cuda.copy_to_host(...).Im folgenden Beispiel (Listing 5) werden sehr viele Daten zwischen Host und GPU hin- und herkopiert. Natürlich sollte man in einen konkreten Kernel die Kopieraktionen so weit wie möglich reduzieren, da diese viel Zeit kosten können und in einigen Fällen die durch die Berechnung auf der GPU gewonnene Zeit durch die Kopieraktionen komplett aufgebraucht wird. Dies passiert meist dann, wenn viele Daten zwischen Host und Device kopiert, aber relativ wenige Rechenoperationen damit ausgeführt werden – wie das im Code von Listing 5 der Fall ist. Dort wird im GPU-Kernel copy_an_array das Array arr1 einfach in das Array arr2 kopiert und mit zwei multipliziert.Listing 5: Kopieren zwischen Host und Device
<span class="hljs-keyword">import</span> numpy <span class="hljs-keyword">as</span> np <br/><span class="hljs-keyword">from</span> numba <span class="hljs-keyword">import</span> cuda <br/><br/># Der CUDA-Kernel kopiert die Daten aus <br/># arr1 <span class="hljs-keyword">in</span> das Array arr2 und mult. mit <span class="hljs-number">2</span> <br/>@cuda.jit <br/>def copy_an_array(arr1, arr2): <br/> pos = cuda.grid(<span class="hljs-number">1</span>) <br/> <br/> <span class="hljs-keyword">if</span> pos &lt; arr1.size and pos &lt; arr2.size: <br/> arr2[pos] = arr1[pos] * <span class="hljs-number">2</span> <br/> <br/># ****** Main Programm ****** <br/>a = np.array([<span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <span class="hljs-number">2</span>, <span class="hljs-number">3</span>, <span class="hljs-number">4</span>, <span class="hljs-number">5</span>]) <br/>b = np.array([<span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>, <span class="hljs-number">0</span>]) <br/><br/># Daten auf GPU kopieren <br/>d_a = cuda.to_device(a) <br/>d_b = cuda.to_device(b) <br/><br/># Kernel ausführen <br/>copy_an_array[<span class="hljs-number">1</span>, <span class="hljs-number">6</span>](d_a, d_b) <br/><br/># Kopierte Daten aus der GPU <span class="hljs-keyword">in</span> <br/># Array c auf dem Host kopieren <br/>c = d_b.copy_to_host() <br/>print(c)
Im Hauptprogramm werden zunächst zwei numpy-Arrays angelegt und initialisiert. Der Befehl d_a = cuda.to_device(a) legt nun in der Größe des Arrays a einen entsprechenden Speicherblock im GPU-Speicher an und kopiert die Daten aus a in diesen Speicher. Die Funktion cuda.to_device liefert ein Objekt vom Typ DeviceNDArray zurück, welches beim Kernel-Aufruf als Parameter übergeben wird. Danach wird die gleiche Aktion für das Array b ausgeführt. Auf diese Weise lässt sich sehr genau kontrollieren, welche Daten kopiert werden, da auch bestimmte Array-Bereiche im Kopierbefehl angegeben werden können.Der Aufruf des Kernels erfolgt mit den beiden DeviceNDArray-Objekten. Nun sollen die Ergebnisdaten explizit in ein Array auf den Host zurückkopiert werden. Hier wird der Befehl c = d_b.copy_to_host() benutzt. Es wird auf dem Host ein neues Array in der erforderlichen Größe erstellt und die Daten werden von der GPU in das neue Array c transferiert.Sie können die GPU-Daten freilich auch in ein existierendes Array kopieren. Dies klappt mit einem leicht modifizierten Kopierbefehl:
<span class="hljs-symbol">d_b.copy_to_host</span>(<span class="hljs-keyword">b) </span>
In diesem Fall werden die Daten aus dem GPU-Array d_b in das bereits existierende Host-Array b übertragen.Wie mit der normalen CUDA-Programmierung stehen auch mit der numba-Bibliothek verschiedene Speichervarianten auf der GPU zur Verfügung. Zusätzlich zum normalen GPU-Speicher kann man das sogenannte Shared Memory benutzen. Dieser Speicher ist in seiner Größe begrenzt, dafür aber sehr schnell. Er lässt sich im Kernel mit cuda.shared.array(...) anlegen. Weiterhin gibt es den lokalen Speicher. Dieser ist ebenfalls in der Größe begrenzt, aber für jeden CUDA-Thread privat. Er wird mit dem Befehl cuda.local.array(...) angelegt. Schließlich gibt es noch den Konstanten-Speicher, den alle Threads gemeinsam nutzen können und der mit cuda.const.array(...) angelegt wird.
Die Matrixmultiplikation
Ein Artikel über Parallelprogrammierung kommt nicht ohne die Implementierung der Matrixmultiplikation [3] aus. In den folgenden Beispielen soll die Multiplikation zweier Arrays in drei Varianten ausgeführt und dabei die Laufzeit gemessen werden.- Normaler Python-Code (ohne irgendwelche Bibliotheken oder anderen Tricks).
- Normaler Python-Code auf der GPU mit numba.
- Benutzung des Shared Memory bei einer blockorientierten Multiplikation auf der GPU.
Listing 6: Matrixmultiplikation mit Python
import numpy as <span class="hljs-built_in">np</span> <br/>import <span class="hljs-built_in">time</span> <br/><br/># Matrixmultiplikation mit Standard- <br/># Python-Code: Es werden normale Schleifen <br/># ohne Bibliotheken <span class="hljs-literal">und</span> anderen Tricks benutzt <br/>def matmul1(A, B, C, n): <br/> <span class="hljs-keyword">for</span> i <span class="hljs-keyword">in</span> <span class="hljs-built_in">range</span>(n): <br/> <span class="hljs-keyword">for</span> j <span class="hljs-keyword">in</span> <span class="hljs-built_in">range</span>(n): <br/> tmp = <span class="hljs-number">0.0</span> <br/> <span class="hljs-keyword">for</span> k <span class="hljs-keyword">in</span> <span class="hljs-built_in">range</span>(n): <br/> tmp += A[i, k] * B[k, j] <br/> <br/> C[i, j] = tmp <br/> <br/>#******************************************* <br/># Main <span class="hljs-built_in">program</span> <br/><br/>n = <span class="hljs-number">512</span> <br/><br/># <span class="hljs-number">3</span> Arrays erzeugen mit Fließkommazahlen <br/>A = <span class="hljs-built_in">np</span>.empty((n, n), dtype=<span class="hljs-built_in">np</span>.float32) <br/>B = <span class="hljs-built_in">np</span>.empty(A.shape, dtype=A.dtype) <br/>C = <span class="hljs-built_in">np</span>.zeros(A.shape, dtype=A.dtype) <br/># Benutzter Speicher <br/>memUse = <span class="hljs-number">3</span> * n * n * <span class="hljs-number">4</span> <br/><br/># Arrays A <span class="hljs-literal">und</span> B mit <span class="hljs-string">"verrückten"</span> Zahlen füllen <br/><span class="hljs-keyword">for</span> i <span class="hljs-keyword">in</span> <span class="hljs-built_in">range</span>(n): <br/> A[i, :] = <span class="hljs-built_in">np</span>.arange(<span class="hljs-number">0.0</span>, <span class="hljs-number">1.0</span>, <span class="hljs-number">1.0</span> / n) + i * <span class="hljs-number">0.01</span> <br/> B[:, i] = <span class="hljs-built_in">np</span>.arange(<span class="hljs-number">1.0</span>, <span class="hljs-number">0.0</span>, -<span class="hljs-number">1.0</span> / n) + i * <span class="hljs-number">0.03</span> <br/><br/># Ausgabe zu Testzwecken <br/><span class="hljs-built_in">print</span>(A) <br/><span class="hljs-built_in">print</span>(B) <br/> <br/>start = <span class="hljs-built_in">time</span>.<span class="hljs-built_in">time</span>() <br/>matmul1(A, B, C, n) <br/>end = <span class="hljs-built_in">time</span>.<span class="hljs-built_in">time</span>() <br/><br/># Ausgabe zu Testzwecken <br/><span class="hljs-built_in">print</span>(<span class="hljs-string">"C[1, 2] = "</span>, C[<span class="hljs-number">1</span>, <span class="hljs-number">2</span>]); <br/><span class="hljs-built_in">print</span>(<span class="hljs-string">"C[7, 3] = "</span>, C[<span class="hljs-number">7</span>, <span class="hljs-number">3</span>]); <br/><span class="hljs-built_in">print</span>(<span class="hljs-string">"C[4, 9] = "</span>, C[<span class="hljs-number">4</span>, <span class="hljs-number">9</span>]); <br/><br/><span class="hljs-built_in">print</span>(<span class="hljs-string">"Zeit: {:6.3f}s"</span>.format(end - start)) <br/><span class="hljs-built_in">print</span>(<span class="hljs-string">"Speicherbelegung: "</span>, memUse / <span class="hljs-number">1024</span>, <span class="hljs-string">"KBytes"</span>)
Die Multiplikation ist in der Funktion matmul1 codiert. In der main-Funktion wird die Größe der Arrays festgelegt, danach werden die Arrays erstellt und mithilfe einer Schleife mit Datenwerten gefüllt. Das Array C wird mit null initialisiert. Die Ausgabe der beiden Arrays A und B dient nur der Kontrolle und lässt sich bei Bedarf auskommentieren. Die Zeiten werden in diesem Beispiel mit time.time() gemessen. Hier ist zu beachten, dass die Funktion unter Microsoft Windows nur eine Genauigkeit von etwa 1/16 Sekunde liefert. In diesen Fall sind die Messzeiten jedoch so lang, dass diese Genauigkeit ausreicht. Nach dem Aufruf von matmult1 werden zur Kontrolle einige Array-Elemente als Ergebnis ausgegeben. Dazu kommen die Rechenzeit in Sekunden und die Speicherbelegung in Kilobyte.In der zweiten Variante soll nun die CUDA-Bibliothek numba zum Einsatz kommen. Da viele Teile des Programms ähnlich wie in Listing 6 sind, sollen in Listing 7 nur die davon abweichenden Teile gezeigt und erläutert werden.Die Kernel-Funktion matmul2 wird nun mit der Präambel @cuda.jit eingeleitet. In der Funktion wird zunächst mit cuda.grid(2) ermittelt, welches Array-Element in diesem Thread berechnet wird. Danach wird geprüft, ob die beiden Indices innerhalb der Array-Größe liegen. Diese Prüfung ist sehr wichtig. Ein Zugriff auf die Speicherbereiche außerhalb des Arrays führt in der Regel zu einem Absturz des Programms. In der inneren k-Schleife wird nun die eigentliche Multiplikation durchgeführt.
Listing 7: Matrixmultiplikation mit CUDA & numba
import numpy as np <br/>import time <br/>from numba import cuda, float32 <br/><br/># Matrixmultiplikation mit Standard- <br/># Code: Es werden normale Schleifen <br/># mit CUDA benutzt <br/>@cuda.jit <br/>def matmul2(d<span class="hljs-emphasis">_A, d_</span>B, d<span class="hljs-emphasis">_C, n): </span><br/><span class="hljs-emphasis"> i, j = cuda.grid(2) </span><br/><span class="hljs-emphasis"> </span><br/><span class="hljs-emphasis"> if i &lt; n and j &lt; n: </span><br/><span class="hljs-emphasis"> tmp = 0.0 </span><br/><span class="hljs-emphasis"> for k in range(n): </span><br/><span class="hljs-emphasis"> tmp += d_</span>A[<span class="hljs-string">i, k</span>] * d<span class="hljs-emphasis">_B[k, j] </span><br/><span class="hljs-emphasis"> </span><br/><span class="hljs-emphasis"> d_</span>C[<span class="hljs-string">i, j</span>] = tmp <br/><br/># Siehe Listing 6! <br/># Nach der Array-Ausgabe... <br/><br/># Vorbereitung des CUDA-Aufrufs <br/>threadsPerBlock = 32 # Maximum ist 32! <br/>blocksPerGrid = (A.shape[<span class="hljs-string">0</span>] + (threadsPerBlock - 1)) // threadsPerBlock <br/> <br/>blockdim = (threadsPerBlock, threadsPerBlock) <br/>griddim = (blocksPerGrid, blocksPerGrid) <br/><br/>#start = time.time() # Zeit mit Daten kopieren <br/>d<span class="hljs-emphasis">_A = cuda.to_</span>device(A) <br/>d<span class="hljs-emphasis">_B = cuda.to_</span>device(B) <br/>d<span class="hljs-emphasis">_C = cuda.to_</span>device(C) <br/><br/>start = time.time() # Zeit ohne Daten kopieren <br/>matmul2[<span class="hljs-string">griddim, blockdim</span>](<span class="hljs-link">d_A, d_B, d_C, n</span>)<br/>end = time.time() # Zeit ohne Daten kopieren <br/>d<span class="hljs-emphasis">_C.copy_</span>to_host(C) <br/>#end = time.time() # Zeit mit Daten kopieren <br/><br/># Siehe Listing 6!
In der main-Funktion gibt es auch einige Änderungen. In der Variablen threadsPerBlock wird die Anzahl der zu benutzenden Threads in einer Dimension festgelegt. Da hier zwei Dimensionen benutzt werden, ist die Gesamtzahl der Threads pro Block 32 * 32 = 1024. Dies ist normalerweise die maximal erlaubte Thread-Anzahl. Nun wird die Anzahl der benötigten Blöcke berechnet und die beiden Tupel für den Aufruf der Kernel-Funktion initialisiert. Im nächsten Schritt werden die Daten aller drei Arrays mit cuda.to_device(...) in den Speicher der GPU kopiert. Die Kernel-Funktion matmul2 wird in der bereits gezeigten Weise mit der Thread- und der Blockanzahl in eckigen Klammern aufgerufen. Als Parameter werden die in der GPU angelegten Arrays d_A, d_B und d_C sowie die Array-Größe n angegeben. Schließlich wird das berechnete Array d_C wieder in den Host-Speicher zurückkopiert und lässt sich dann ganz normal weiterverarbeiten.In der dritten Variante soll das Shared Memory der GPU genutzt werden, um den Code noch weiter zu beschleunigen. Der hier angewendete Trick ist allgemein bekannt. Es wird ein kleines Array im schnellen Speicher angelegt und die Daten werden blockweise mithilfe dieser kleinen – aber schnellen – Arrays verarbeitet.Listing 8 zeigt die neue Kernel-Funktion matmul3. Die main-Funktion ist die gleiche wie in Listing 7.
Listing 8: Matrixmultiplikation mit Shared Memory der GPU
SIZE = <span class="hljs-number">32</span> <br/><br/># Matrixmultiplikation mit speziellem <br/># Code: Es wird der schnelle Speicher <br/># mit CUDA benutzt <br/>@cuda.jit <br/>def matmul3(d_A, d_B, d_C, n): <br/> # Definition der kleineren Shared-Arrays <br/> # im schnellen Speicher <br/> sA = cuda.shared.array(<br/> shape=(SIZE, SIZE), dtype=float32) <br/> sB = cuda.shared.array(<br/> shape=(SIZE, SIZE), dtype=float32) <br/><br/> i, j = cuda.grid(<span class="hljs-number">2</span>) <br/> tx = cuda.threadIdx.x <br/> ty = cuda.threadIdx.y <br/> blocksPerGrid = cuda.gridDim.x # Blöcke / Grid <br/> <br/> <span class="hljs-keyword">if</span> i &gt;= n or j &gt;= n: <br/> # Außerhalb der Array-Grenzen <br/> return <br/><br/> # Multiplikation der kleinen Arrays <br/> tmp = <span class="hljs-number">0.0</span> <br/> <br/> for k <span class="hljs-keyword">in</span> range(blocksPerGrid): <br/> # Daten <span class="hljs-keyword">in</span> die kleinen Arrays laden <br/> sA[tx, ty] = d_A[i, ty + k * SIZE] <br/> sB[tx, ty] = d_B[tx + k * SIZE, j] <br/><br/> # Warten, bis die Kopieraktion erledigt ist <br/> cuda.syncthreads() <br/> <br/> # Teilergebnisse berechnen <br/> for kk <span class="hljs-keyword">in</span> range(SIZE): <br/> tmp += sA[tx, kk] * sB[kk, ty] <br/><br/> # Warten, bis alle Threads fertig sind <br/> cuda.syncthreads() <br/><br/> # Ergebnis speichern <br/> d_C[i, j] = tmp
Die beiden Hilfsarrays sA und sB werden mit dem Befehl cuda.shared.array(...) angelegt. Die Größe dieser Arrays ist als Compiler-Konstante size vorher festzulegen. Nun wird in den Variablen i und j ermittelt, welches Array-Element berechnet werden soll. Außerdem wird in den Variablen tx und ty bestimmt, welcher Datenblock in den beiden Hilfs-Arrays gerade in Benutzung ist.Im Grunde genommen sind nun zwei unabhängige Operationen auszuführen. Zunächst werden die benötigten Datenelemente aus den großen Arrays in die kleinen Hilfsarrays kopiert. Erst wenn diese Aktion vollendet ist, beginnt die Berechnung des Array-Elements d_C[i, j]. Ist diese Berechnung abgeschlossen, können die nächsten Datenblöcke verarbeitet werden. Wie man unschwer erkennen kann, müssen diese Operationen synchronisiert werden, das heißt, jede Operation muss abgeschlossen sein, bevor es weitergeht. Dies gewährleisten die beiden Aufrufe von cuda.syncthreads(). Die Threads, die ihre Aufgabe bereits beendet haben, warten an der Stelle, bis alle Threads fertig sind. Diese Synchronisierungsvariante wird auch als Barriere (barrier) bezeichnet.In der kk-Schleife wird nun das jeweilige Array-Element mithilfe der beiden schnellen Hilfs-Arrays berechnet und im Ergebnis-Array abgelegt. Die main-Funktion des Beispiels arbeitet wie die aus Listing 7.An dieser Stelle sollen nun auch einige Performance-Ergebnisse gezeigt werden. Bitte beachten Sie hier unbedingt, dass diese Ergebnisse sehr stark von der jeweils benutzen Hardware abhängen. Die Rechenzeit für die Matrixmultiplikation ist abhängig von der Anzahl der Threads, die eine Grafikkarte gleichzeitig laufen lassen kann. Auch das Tempo der Datenübertragung zwischen Host (CPU) und Device (GPU) kann von Rechner zu Rechner sehr unterschiedlich sein. Bild 1 zeigt die auf einem einfachen Notebook mit einer normalen Nvidia-GeForce-Grafikkarte vorgenommenen Messungen. Die verwendeten Arrays hatten eine Größe von 512 * 512 Elementen.
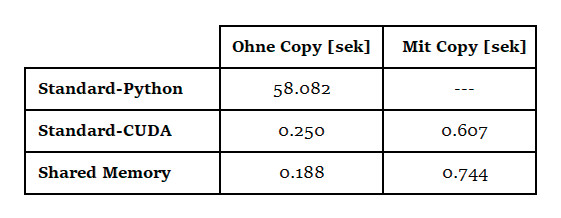
Gemessene Laufzeitenfür die drei Varianten der Matrixmultiplikation(Bild 1)
Autor
Es ist gut zu erkennen, dass die Übergabe der Daten an die GPU ein sehr entscheidender Faktor in Sachen Laufzeit der Berechnung ist. Trotzdem ist der Performance-Gewinn in beiden Fällen durchaus positiv zu bewerten. Vor allem die Variante Standard-CUDA, die ja sehr einfach zu programmieren ist, liefert hervorragende Ergebnisse.
Zusammenfassung
Die Benutzung von CUDA mit C und C++ ist nicht gerade einfach. Nutzt man dagegen Python, gibt es viele angenehme Vereinfachungen. Automatisches Kopieren von Arrays in den Kernel, einfaches Ermitteln der Thread-Nummern und normale Python-Programmierung in der Kernel-Funktion sind nur einige davon.Da Python als Skriptsprache eher langsam ist, bietet die Bibliothek numba hier große Performance-Steigerungen – besonders dann, wenn in den diversen Python-Bibliotheken keine schnellen C-Implementierungen für das zu lösende Problem vorhanden sind. Trotzdem muss man bei der Benutzung von CUDA immer die Dauer der Datenübertragung im Auge behalten. Außerdem sollte die Menge der zu verarbeitenden Daten ausreichend groß sein, damit sich eine Geschwindigkeitsverbesserung ergeben kann.Fussnoten
- Bernd Marquardt, Vollgas mit der GPU, Teil 1, Rechnen mit CUDA, dotnetpro 4/2019, Seite 68 ff., http://www.dotnetpro.de/A1904Cuda
- CUDA Download, http://www.dotnetpro.de/SL1905CUDA1
- Matrizenmultiplikation, http://www.dotnetpro.de/SL1905CUDA2
