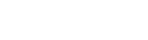18. Apr 2022
Lesedauer 8 Min.
Überschwingen ade
Fuzzylogik, Teil 2
Der PI-Fuzzy-Regler regelt Prozesse dynamisch und verfügt über ein Fluent Interface.
dotnetpro
Der erste Artikel hat die Grundprinzipien anhand eines Raumtemperaturreglers erklärt [1]. Dieses Wissen wird nun eingesetzt, um einen universalen Fuzzylogik-Regler zu modellieren, dessen dynamisches Verhalten sich gezielt auf den zu regelnden Prozess zuschneiden lässt. Dazu erhält der Regler ein Fluent Interface, implementiert in C#. Die Resultate werden mit einem klassischen PID-Regler verglichen.Der PID-Regler ist wohl der bekannteste Regler; PID steht für Proportional Integral Derivative [2]. Der P-Anteil regelt die Stellgröße proportional zur Sollwert-Istwert-Abweichung: Je größer die Abweichung, desto größer die Stellgröße. Wenn die Sollwert-Istwert-Abweichung 0 und der Prozess stabil ist, dann enthält der I-Anteil die Stellgröße, die nötig ist, um eventuelle Verluste zu kompensieren.Eine Aufgabe des D-Anteils ist, zu verhindern, dass der Istwert am Sollwert vorbeischießt (overshoot oder undershoot). Das passiert typischerweise nach großen Sollwert-Istwert-Abweichungen, etwa nach Einschalten eines Systems. Der D-Anteil muss schnell auf Sollwert-Istwert-Änderungen reagieren. Das können Störungen sein (wenn etwa eine Ofentür geöffnet wird), aber auch Sollwert-Änderungen, beispielsweise wenn die Soll-Temperatur durch den Nutzer erhöht wird.Diese dynamischen Anforderungen werden beim klassischen PID-Regler nur mit einem Parameter, dem D-Anteil, abgedeckt. Hinzu kommt, dass der Regler linear arbeitet, aber die Regelstrecke meistens nicht linear ist. Deshalb erfordert die Einstellung des PID-Reglers Kompromisse.Da vor allem die Dynamik der Strecke Probleme bereitet, wäre es sehr hilfreich, den D-Anteil je nach Regelbereich unterschiedlich einstellen zu können. Genau das ist mit dem PI-Fuzzy-Regler möglich.
Korrekturen zum ersten Teil der Artikelserie [1]
Leider hatten sich im ersten Teil zwei Fehler eingeschlichen. In Bild 3 fehlt an der y-Achse der Wert 1,0. Die letzten beiden Sätze müssen lauten: „Bei dem klassischen PID-Regler werden die unterschiedlichen dynamischen Regler-Anforderungen eines Prozesses nur mit einem Parameter, dem D-Anteil, abgedeckt. Der zu modellierende PI-Fuzzy-Regler ermöglicht es, das dynamische Regelverhalten gezielt auf den Prozess abzustimmen.“
Der PI-Fuzzy-Regler
Das Resultat des Fuzzylogik-Teils dieser Lösung ist – das sei schon vorweggenommen – eine zweidimensionale Tabelle, welche die Abweichung und deren Änderung einem Steuerwert zuordnet. Diese Tabelle lässt sich nach der Modellierung also direkt auf dem Zielsystem implementieren. Das ist gut zu wissen, wenn die Zielplattform eingeschränkte Ressourcen hat oder der Reglerzyklus extrem schnell sein soll.Den Aufbau des Reglers stellt Bild 1 dar. Der Sollwert wird vom Istwert abgezogen und dient als „scharfer Wert“ für die linguistische Variable Error. Ein negativer Wert bedeutet also, dass der Istwert zu klein ist. Die Variable Change bildet die Änderung von Error in der Zeit ab. Die beiden werden später mit Wissensregeln verknüpft und sorgen für die P- und D-Aktion.
Der Aufbaudes PI-Fuzzy-Reglers(Bild 1)
Autor
Solange der Steuerwert sich im Regelbereich befindet (zwischen -100 und +100 Prozent oder 0 und 100 Prozent, je nach Anwendung) wird eine Fraktion (I-Faktor) von Error integriert und zum Endresultat addiert (oder subtrahiert, wenn der I-Anteil negativ ist). Der I-Anteil ist in diesem Regler also rein klassisch implementiert. Die Fuzzy-Sets des Reglers sind in Bild 2 zu sehen. Alle Zugehörigkeitsfunktionen sind symmetrisch, komplementär und normalisiert. Der Regelbereich für Error und Change liegt zwischen -2 und 2. Mit einem P- und D-Faktor werden die Eingangsgrößen Error und Change vor dem Fuzzyfizieren skaliert, sodass sie in den Regelbereich passen.
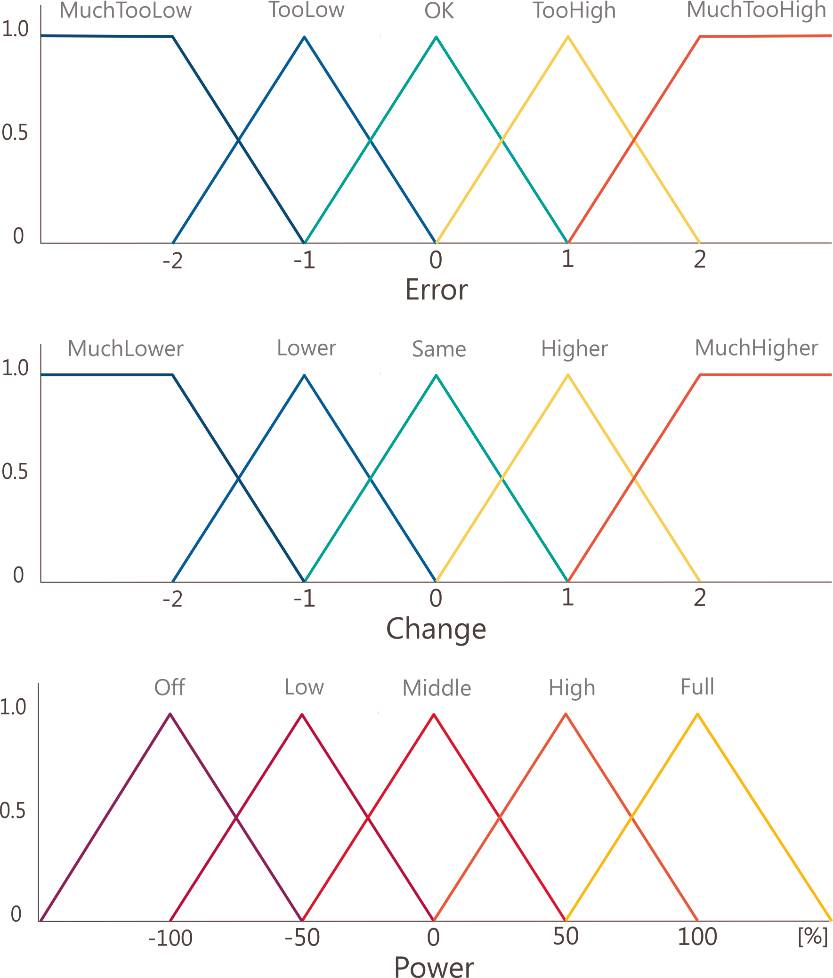
Die Fuzzy-Setsdes PI-Fuzzy-Reglers(Bild 2)
Autor
Mit diesen Fuzzy-Sets lässt sich nun das Regelwerk des Reglers zusammenstellen.
Regeln für den P-Anteil
Als erste Regeln sind hier die für den P-Anteil genannt:1x IF Error = MuchTooLow THEN Power = Full
1x IF Error = TooLow THEN Power = High
1x IF Error = OK THEN Power = Middle
1x IF Error = TooHigh THEN Power = Low
1x IF Error = MuchTooHigh THEN Power = Off
Solange alle Regeln das gleiche Gewicht haben, ist das Verhalten linear. Je nach System ist es wünschenswert, dass der Regler sich in einem Bereich um den Nullpunkt ruhiger verhält, um zum Beispiel mechanischen Verschleiß zu minimieren. Das lässt sich erreichen, indem die Regel „IF OK Then Middle“ eine stärkere Gewichtung erhält. Hat die Regel das Gewicht 3, dann sieht die Übertragung aus wie in Bild 3.
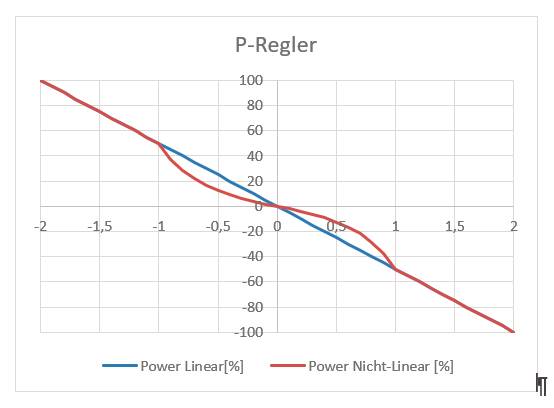
Der Fuzzy-P-Reglermit stärkerer Gewichtung im Nullbereich(Bild 3)
Autor
Regeln gegen Überschwingen
Überschwingen (overshoot) oder Unterschwingen (undershoot) tritt ein, wenn der Istwert sich weit außerhalb des Regelbereichs befindet und der Regler den Istwert mit maximalem Stellwert Richtung Sollwert steuert.Gelangt der Istwert in den Regelbereich, bedarf es Maßnahmen, um sozusagen den rollenden Ball zu stoppen, sonst besteht die Gefahr, dass der angestrebte Wert am Ziel vorbeischießt. Dies passiert zum Beispiel, wenn mit einem Achsensystem oder beim Aufheizen eines Ofens eine Position schnell angefahren werden soll.Um Überschwingen zu vermeiden, gibt es einige nichtlineare Tricks. Der PI-Fuzzy-Regler hat für diesen Fall vier Wissensregeln, die diese Situation erkennen und ihr entgegenwirken. Dem Überschwingen begegnen folgende Regeln:2x IF Error = TooLow AND Change = MuchHigher
THEN Power = Low
2x IF Error = OK AND Change = MuchHigher
THEN Power = Off
Ein Unterschwingen dämpft er so:
2x IF Error = TooHigh AND Change = MuchLower
THEN Power = High
2x IF Error = OK AND Change = MuchLower
THEN Power = Full
Mit der Gewichtung (hier 2x) lässt sich Einfluss der einzelnen Regeln bestimmen. Der Regelbereich muss dennoch groß genug sein, um ein Überschießen zu verhindern.
Dämpfung
Um Schwingungen und Störungen entgegenzuwirken, kann man ein paar Regeln zum Regelwerk hinzufügen, die rund um die Nullabweichung aktiv sind. Stellen Sie sich vor, dass in einer Fritteuse das Öl auf Temperatur erhitzt ist und gefrorene Ware hineingelegt wird; oder ein Industrieofen ist aufgeheizt und die Ofentür wird geöffnet. Ein Sollwert, der sich sprungartig ändert, lässt sich mit diesen Regeln abfangen:2x IF Error = TooLow AND Change = Lower
THEN Power = Full
2x IF Error = TooLow AND Change = Same THEN Power = Full
2x IF Error = OK AND Change = Lower THEN Power = High
2x IF Error = OK AND Change = Higher THEN Power = Low
2x IF Error = TooHigh AND Change = Same THEN Power = Off
2x IF Error = TooHigh AND Change = Higher
THEN Power = OFF Implementierung
Der Regler wird mit Fluent Interfaces in C# implementiert. Dabei ist anzumerken, dass C# mit seiner Speicherbereinigung in Kombination mit Windows nicht gerade ideale Voraussetzungen für eine Regelung im Echtzeitbereich bietet. Für nicht zeitkritische Prozesse und zu Demonstrationszwecken wie diese reichen die gewählten Technologien aber aus.Die Fuzzy-Sets
Der Regler arbeitet mit zwei Fuzzy-Sets für die Eingänge (FuzzySetError und FuzzySetChange) und einem Fuzzy-Set für den Ausgang (Stellwert FuzzySetOutput). Da alle Zugehörigkeitsfunktionen dreieckförmig und komplementär sind, genügt es, für jede Funktion das Maximum zu definieren. Im Grunde sind alle Zugehörigkeitsfunktionen einfache Singletons. Während der Fuzzyfizierung wird für jede Eingangsfunktion der Zugehörigkeitsgrad (Wahrheitsgrad) berechnet und zur Funktion gespeichert.Für die Fuzzy-Sets der Eingänge sieht eine Zugehörigkeitsfunktion so aus:public class MemberFunc
{
public double Max { get; set; }
public double Degree { get; set; }
}
Das Fuzzy-Set für die Eingangsvariable Error ist in Listing 1 dargestellt.
Listing 1: Fuzzy-Set für die Variable Error
public class FuzzySetError <br/>{ <br/> private readonly MemberFunc[] _memberFuncs = { <br/> new MemberFunc{Max = -2.0}, <br/> new MemberFunc{Max = -1.0}, <br/> new MemberFunc{Max = 0.0}, <br/> new MemberFunc{Max = 1.0}, <br/> new MemberFunc{Max = 2.0} <br/> }; <br/><br/> public MemberFunc[] MemberFuncs =&gt; _memberFuncs; <br/> public double MuchTooLow =&gt;<br/> _memberFuncs[0].Degree; <br/> public double TooLow =&gt; _memberFuncs[1].Degree; <br/> public double Ok =&gt; _memberFuncs[2].Degree; <br/> public double TooHigh =&gt; _memberFuncs[3].Degree; <br/> public double MuchTooHigh =&gt;<br/> _memberFuncs[4].Degree; <br/>}
Die einzelnen Eigenschaften vereinfachen die Lesbarkeit im Sinne einer DSL, einer Domain Specific Language; die Eigenschaft Memberfuncs wird für die Fuzzyfizierung benötigt.Das Fuzzy-Set für die Ausgangsvariable wird geprägt durch Einfachheit, da die einzelnen Zugehörigkeitsfunktionen keine Wahrheitsgrade brauchen:
class FuzzySetOutput
{
public double PowerOff => -100.0;
public double PowerLow => -50.0;
public double PowerMiddle => 0.0;
public double PowerHigh => 50.0;do
public double PowerFull => 100.0;
} Fuzzyfizierung
Zuerst müssen die Eingangsvariablen Error und Change fuzzyfiziert werden. Weil die Zugehörigkeitsfunktionen komplementäre (die Summe ist immer eins) Dreiecke sind (eigentlich Singletons), werden die Zugehörigkeitsgrade durch einfache lineare Interpolation berechnet (Listing 2).Listing 2: Berechnung der Zugehörigkeitsgrade
private void Fuzzificate(double value, MemberFunc[] <br/> memberFuncs) <br/>{ <br/> foreach (MemberFunc fuzzySet in memberFuncs) <br/> { <br/> fuzzySet.Degree = 0.0; <br/> } <br/> // Below lower range <br/> if (value &lt;= memberFuncs[0].Max) <br/> { <br/> memberFuncs[0].Degree = 1.0; <br/> return; <br/> } <br/> // Assign degrees of truth <br/> for (int i = 0; i &lt; memberFuncs.Length - 1; i++) <br/> { <br/> if (value &gt; memberFuncs[i].Max &amp;&amp;<br/> value &lt;= memberFuncs[i + 1].Max) <br/> { <br/> memberFuncs[i].Degree =<br/> (memberFuncs[i + 1].Max - value) /<br/> (memberFuncs[i + 1].Max<br/> - memberFuncs[i].Max); <br/> memberFuncs[i + 1].Degree =<br/> 1.0 - memberFuncs[i].Degree; <br/> return; <br/> } <br/> } <br/> // Above upper range <br/> memberFuncs[memberFuncs.Length - 1].Degree = 1.0; <br/>}
Die Aufrufe der Fuzzyfizierung haben das folgende Aussehen:
public void Fuzzificate(double error, double change)
{
...
Fuzzificate(error, _fuzzySetError.MemberFuncs);
Fuzzificate(change, _fuzzySetChange.MemberFuncs);
} Regelwerk mit Fluent Interfaces
Das Konzept des Fluent Interface (Fluent-API) ist das Mittel par excellence, um das nötige Regelwerk zu definieren. Mit einem Fluent Interface (auf Deutsch „flüssige Schnittstelle“ oder „sprechende Schnittstelle“) lassen sich komplexe Abläufe im Programmcode wie Sätze in natürlicher Sprache formulieren. Die dazu definierten Methoden bilden die DSL für die Fuzzylogik.Um das Fluent-API umzusetzen, wird sogenanntes Method Chaining eingesetzt. Bei dieser Technik gibt jede Methode eine Objektinstanz zurück und alle solche Methoden können zu einer einzigen Anweisung verkettet werden.Das Regelwerk des PI-Fuzzy-Reglers (Listing 3) sieht mit einem Fluent-API sehr natürlich aus: Die Instanz fuzzyFluent definiert alle Fluent-Methoden und verwaltet einige interne Variablen für die Berechnung. Die Defuzzyfizierung erfordert einen Zähler und einen Nenner, die am Anfang jedes Berechnungszyklus auf 0 gesetzt werden.Listing 3: Das Regelwerk des PI-Fuzzy-Reglers
// Proportional <br/>fuzzyFluent.Weight(1.0).IfMuchTooLow().<br/> ThenPowerFull(); <br/>fuzzyFluent.Weight(1.0).IfTooLow().ThenPowerHigh(); <br/>fuzzyFluent.Weight(1.0).IfOk().ThenPowerMiddle(); <br/>fuzzyFluent.Weight(1.0).IfTooHigh().ThenPowerLow(); <br/>fuzzyFluent.Weight(1.0).IfMuchTooHigh().<br/> ThenPowerOff(); <br/>// Minimize Overshoot <br/>fuzzyFluent.Weight(2.0).IfTooLow().AndMuchHigher().<br/> ThenPowerLow(); <br/>fuzzyFluent.Weight(2.0).IfOk().AndMuchHigher().<br/> ThenPowerOff(); <br/>// Minimize Undershoot <br/>fuzzyFluent.Weight(2.0).IfTooHigh().AndMuchLower().<br/> ThenPowerHigh(); <br/>fuzzyFluent.Weight(2.0).IfOk().AndMuchLower().<br/> ThenPowerFull(); <br/>// Damping <br/>fuzzyFluent.Weight(2.0).IfTooLow().AndLower().<br/> ThenPowerFull(); <br/>fuzzyFluent.Weight(2.0).IfTooLow().AndSame().<br/> ThenPowerFull(); <br/>fuzzyFluent.Weight(2.0).IfOk().AndLower().<br/> ThenPowerHigh(); <br/>fuzzyFluent.Weight(2.0).IfOk().AndHigher().<br/> ThenPowerLow(); <br/>fuzzyFluent.Weight(2.0).IfTooHigh().AndSame().<br/> ThenPowerOff(); <br/>fuzzyFluent.Weight(2.0).IfTooHigh().AndHigher().<br/> ThenPowerOff();
Die Methode Weight() speichert das Gewicht der Wissensregel in einer internen Variablen:
public FuzzyFluent Weight(double weight)
{
_weightIntern = weight;
return this;
}
Die nächste Fluent-Methode stellt die P-Komponente des Reglers dar; diese speichert den Wahrheitsgrad einer Zugehörigkeitsfunktion vom Eingang Error in einer internen Variablen:
public FuzzyFluent IfMuchTooLow()
{
_degreeIntern = _fuzzySetError.MuchTooLow;
return this;
}
Für die Wissensregeln, die den dynamischen Anteil des Reglers bilden, folgt eine eigene Fluent-Methode. Sie speichert das Minimum des Wahrheitsgrads einer Zugehörigkeitsfunktion vom Eingang Change und des bereits zwischengespeicherten berechneten Zugehörigkeitsgrads:
public FuzzyFluent AndMuchLower()
{
_degreeIntern = Math.Min(_degreeIntern,
_fuzzySetChange.MuchLower);
return this;
}
Die letzte Methode für das Fluent Interface ist zuständig für die Ausgangsvariable. Sie kombiniert die zwischengespeicherten Werte und addiert sie zum Zähler und Nenner:
public void ThenPowerFull()
{
_numerator += _weightIntern * _degreeIntern *
_fuzzySetOutput.PowerFull;
_denominator += _weightIntern * _degreeIntern;
} Defuzzyfizierung
Die Summe aller Wissensregeln spiegelt sich nun im Zähler und Nenner wider. Die Defuzzyfizierung ist nicht mehr als die Division der beiden (Listing 4).Listing 4: Die Defuzzyfizierung
public double Output <br/>{ <br/> get <br/> { <br/> if (_denominator &gt; 0.001) <br/> { <br/> return _numerator / _denominator; <br/> } <br/> else if((_numerator &lt;= 0 &amp;&amp;<br/> _denominator &gt;= 0) || <br/> (_numerator &gt;= 0 &amp;&amp; _denominator &lt;= 0)) <br/> { <br/> return -100.0; <br/> } <br/> return 100.0; <br/> } <br/>} Aufbereitung des Stellwerts
Der Fuzzylogik-Regler liefert einen Stellwert zwischen -100 und 100 Prozent für den proportionalen und dynamischen Teil des Reglers. Zu diesem Wert ist noch ein Integrator zu addieren. Dieser berechnet den Stellwert, um die Prozessverluste zu kompensieren, wenn das System in Gleichgewicht ist (Sollwert gleich Istwert und keine Änderungen).Als letzter Schritt soll dann noch der Stellwert auf Werte zwischen -100 und 100 Prozent oder 0 und 100 Prozent begrenzt werden.Der Vergleich
Um die PI-Fuzzy- und PID-Regler zu vergleichen, soll das Modell eines Gasofens herangezogen werden. Die Leistung von dessen Gasbrenner wird mit einer Stellgröße zwischen 0 und 100 Prozent bestimmt (dabei gibt es keine Kühlung, allein die Wärmeverluste dienen zur Kühlung). Die Simulation ist ein Modell zweiter Ordnung mit den Zeitkonstanten 1500 und 3000 Sekunden, einer Totzeit von 60 Sekunden und einer statischen Verstärkung mit dem Faktor 13,5. Der Prozess ist so langsam, dass eine Sample-Rate von 20 Sekunden genügt.Bild 4 zeigt, wie der PI-Fuzzy-Regler später allerdings aggressiver reagiert, wenn der Istwert sich dem Sollwert beim Start des Systems nähert. Es gibt minimale Schwingungen, die einen Überschuss minimieren.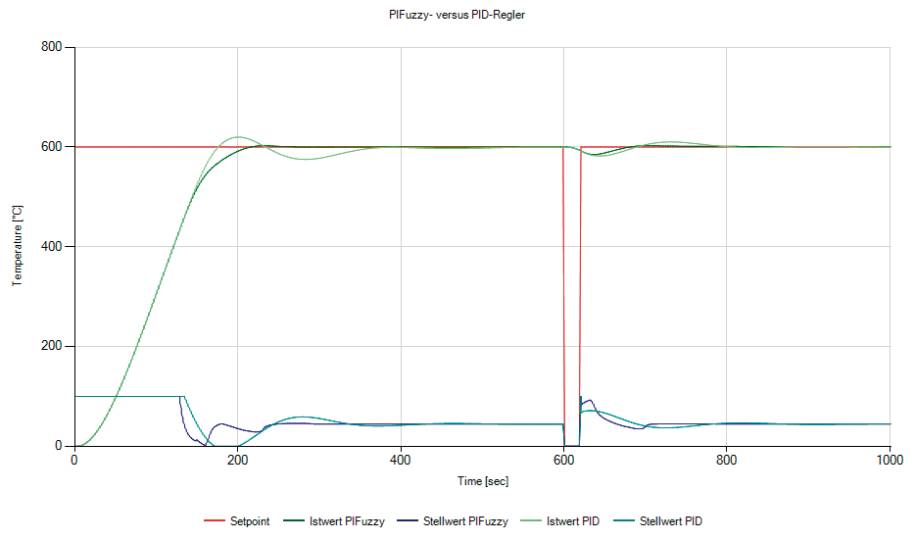
PI-Fuzzy-versus PID-Regler(Bild 4)
Autor
Auch nach einer Störung (simuliert durch einen temporären Sollwerteinbruch) erholt sich der Istwert mit dem PI-Fuzzy-Regler schneller.Die Verluste werden durch die beiden Regelalgorithmen auf gleiche Weise mit der klassischen Implementierung des Integrators kompensiert.
Zusammenfassung
Dieser Artikel und sein Vorgänger in der vorherigen Augabe der dotnetpro haben gezeigt, dass Fuzzylogik nach wie vor in den Werkzeugkasten eines Entwicklers gehört. Diese Technologie macht es möglich, auf pragmatische Weise komplexe Probleme zu lösen, und sie lässt sich einfach mit anderen Technologien wie neuralen Netzen kombinieren.Ein Fluent-API ermöglicht es, eine DSL-Basis (Domain Specific Language) zu gestalten, was die Implementation noch natürlicher macht. Und vielleicht führt dieser Artikel ja dazu, Fuzzylogik aus dem Ruhestand zu holen.Fussnoten
- Erik Stroeken, Unscharf zur ruckelfreien U-Bahn, Fuzzylogik – Teil 1, dotnetpro 4/2022, Seite 88 ff., http://www.dotnetpro.de/A2204Fuzzy
- Wie funktioniert ein PID-Regler? Eine nicht-wissenschaftliche Erklärung, http://www.dotnetpro.de/SL2205Fuzzy1
