12. Jun 2023
Lesedauer 12 Min.
Lineare Regression für Einsteiger
Grundlagen der KI
Eine Trendlinie errechnen, die eine Aussage über die Zukunft ermöglicht.

Das Leben würzt den Alltag mit gewichtigen Fragen, deren Beantwortung nicht einer gewissen Dringlichkeit entbehrt. Wann zum Beispiel geht Ihnen das Klopapier aus? Hätte Ihnen jemand in der Oberstufe erklärt, dass Sie statische Verteilungen eines Tages als Grundlagenmathematik für die Berechnung dieses Zeitpunkts einsetzen, hätten Sie bestimmt besser aufgepasst.Aber es ist nicht aller Tage Abend: Einmal angenommen, Sie hätten Lust darauf, ein wenig mehr von der Mathematik dahinter zu verstehen, dann wären Sie hier genau richtig. Gleichzeitig erfahren Sie dadurch aber auch, wie denn nun KI im Innersten funktioniert.
;tldr
Der Begriff Lineare Regression beschreibt in der Statistik ein Verfahren, mittels dessen es Ihnen gelingt, zu gesammelten Daten, die sich zweidimensional darstellen lassen, einen linearen Verlauf zu ermitteln. Dafür benötigt es eine Steigungsfunktion – und die zu berechnen erfordert einiges an Mathematik, die Ihnen in diesem Artikel anschaulich erklärt werden wird.
Mathematik
Wenn Sie sich an Ihren Mathematikunterricht zurückerinnern, werden Ihnen Begriffe wie Kurvendiskussion, lineare Algebra und dergleichen mehr ins Gedächtnis springen. Für diesen Artikel benötigen Sie das Wissen rund um lineare Funktionen und auch Ableitungen sowie – in dem Kontext – die Berechnung von Grenzwerten, wobei sich Letzteres dramatischer anhört, als es in diesem Fall ist.Der Grund? Es geht darum, lineare Verläufe zu berechnen, um so wahrscheinliche zukünftige Datenpunkte vorhersehen zu können. Was das bedeutet, soll gleich klar werden.Ein kleiner Hinweis noch, bevor es losgeht: In diesem Artikel wird bewusst auf zu viel Fachterminologie verzichtet. Zum einen finden sich auch in der Literatur nicht selten zwei oder mehr unterschiedliche Begriffe für die gleiche Sache, und zum anderen genügt es, mit Ihrem Schulwissen und -vokabular den Zusammenhang zu den Grundlagen der heutigen KI-Forschung zu erschließen.Meet Spence
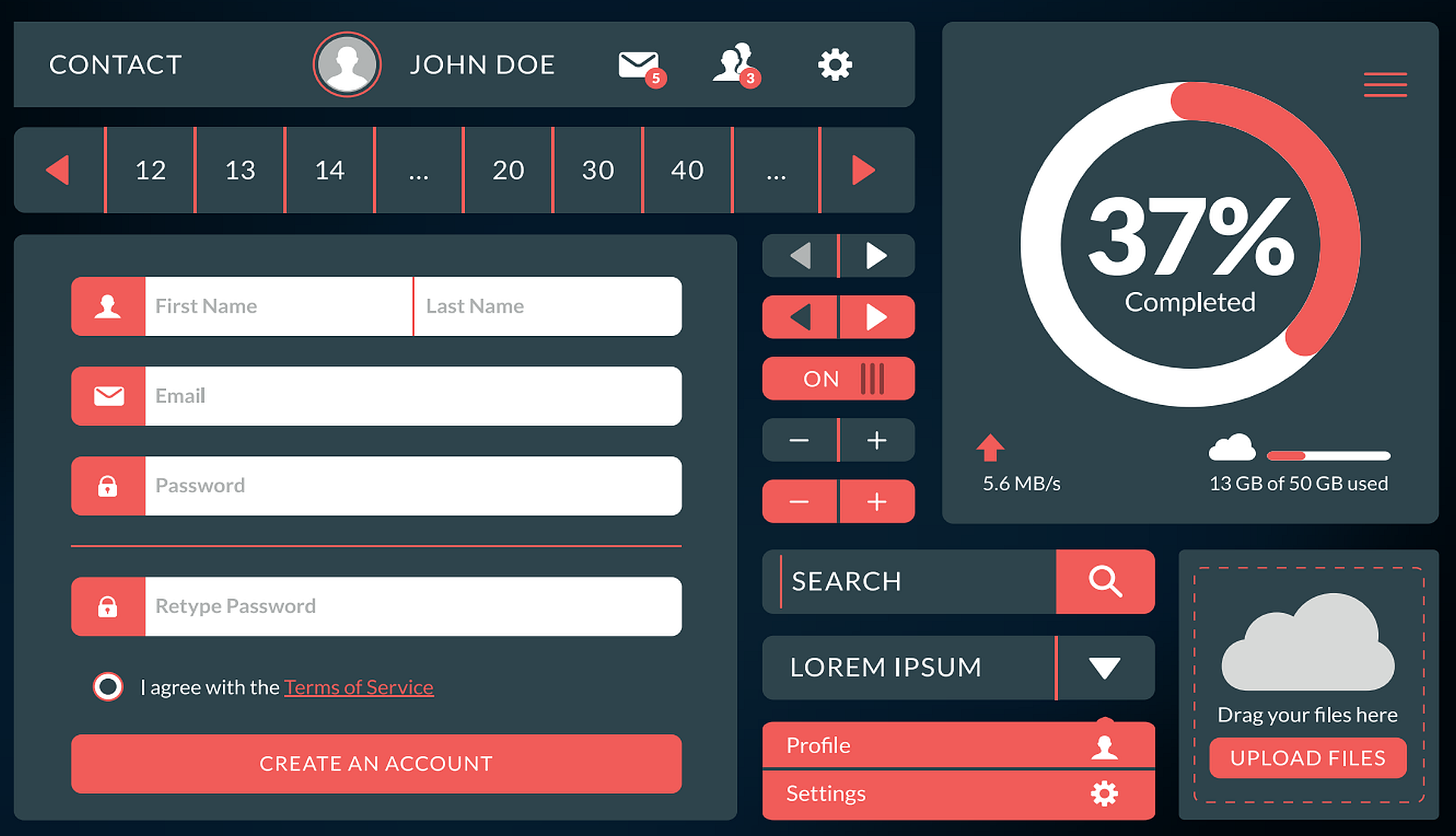
Damit es Ihnen sogar noch leichter fällt, den hier angestellten Überlegungen zu folgen, gibt es zunächst ein praktisches Beispiel inklusive Case-Szenario. In diesem Fall stellen Sie sich eine App vor – sie trägt den Namen „Spence“.Bei Spence handelt es sich um einen Helfer, der auf keinem Smartphone fehlen sollte. Das Motto: Wenn Sie es kaufen können, kann Spence es auch! Wo andere Apps aber aufhören, fängt Spence erst richtig an: Denn Spence versteht, dass es Produkte des täglichen Bedarfs gibt, die Sie regelmäßig kaufen, und nach kurzer Zeit schon bitten Sie nicht mehr Spence, den Vorrat an Klopapier aufzustocken, sondern Spence fragt Sie, ob noch genug Klopapier im Haus ist! Wenn Sie das schon verwundert – denn Spence liegt fast immer richtig –, werden Sie erstaunt sein, wenn – im Rahmen des von Ihnen freigegebenen Budgets – Spence damit beginnt, neues Klopapier zu bestellen, noch bevor die letzte Rolle angebrochen wurde. Doch wie macht Spence das?Zunächst einmal: Wie bei jeder anderen KI auch liegt der Schlüssel in den Daten. Jedes Mal, wenn Sie auf dem stillen Örtchen – das Smartphone in der Hand – durch Ihre konfigurierten Produkte scrollen und beim Klopapier kurz halt machen, um auf den Restock-Button zu drücken, lösen Sie am Ende des Tages nicht einfach nur eine manuelle Bestellung aus. Spence merkt sich das Produkt und den Zeitpunkt der Bestellung. Mit jeder Bestellung entsteht damit eine Datensammlung (Tabelle 1), aus der sich ablesen lässt, wie groß die Intervalle dazwischen sind. Natürlich schwanken diese. Bild 1 zeigt die Werte von Tabelle 1 in einem Graphen an.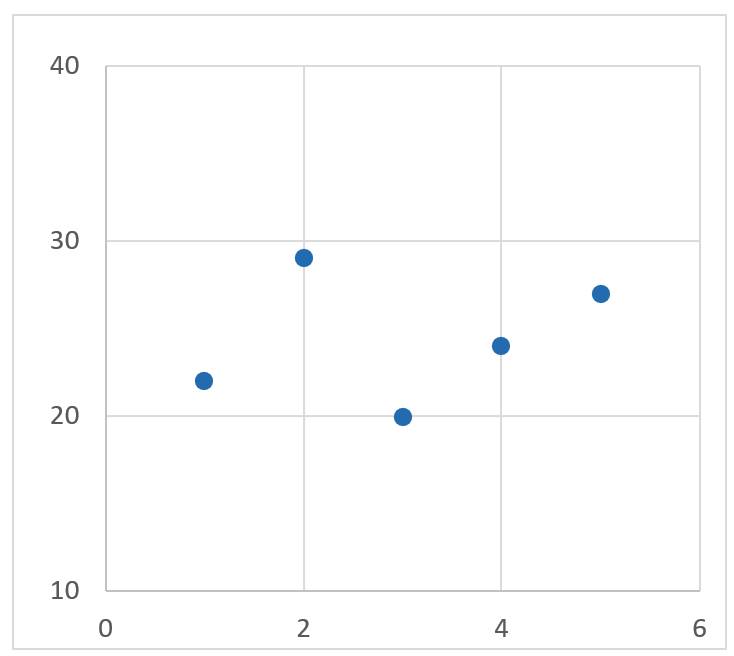
Die Werte von Tabelle 1:Wann wurde Klopapier bestellt?(Bild 1)
Autor
Zu simpel?
Falls Sie sich schon ein wenig mehr mit der Grundlagenmathematik hinter dem Thema der linearen Regression auskennen, werden Sie auf Anhieb überlegen, ob an dieser Stelle eine Durchschnittsrechnung nicht ausreichen würde. Sie hätten damit nicht ganz Unrecht. Für diesen Artikel aber wurde das Beispiel ein wenig vereinfacht, um sich nicht zu sehr in Datenmengen zu verzetteln – aber dazu später mehr.Die Aussage der Werte
Was sagt die Tabelle aus? Nun, im Grunde genommen gibt sie zunächst einmal wieder, dass Sie zu verschiedenen Zeitpunkten eine Nachbestellung ausgelöst haben. Um diese Daten zweidimensional auf zwei Achsen verteilen zu können, gibt es abhängig vom jeweiligen Datum eine Aussage darüber, wie viele Tage zwischen den Bestellungen lagen. Somit gibt es zwei Datenpunkte: Auf der x-Achse den jeweiligen Messpunkt und auf der y-Achse die Anzahl an Tagen, die zwischen zwei Messpunkten liegt.Angenommen, Sie fänden eine lineare Gleichung, die eine Gerade bildet, die möglichst dicht an allen Messpunkten dran wäre, dann könnten Sie eine Vorhersage darüber treffen, wann die nächsten Messpunkte zu erwarten wären. Oder etwas weniger mathematisch ausgedrückt: Wann es sich lohnt, das Klopapier nachzubestellen.Um an dieser Stelle noch einmal kurz auf den Einschub von oben zu sprechen zu kommen: Ja, das klingt simpel. Mit Absicht. Andere Beispiele – sollten Sie im Internet nach dem Thema suchen – ziehen Ideen heran wie zum Beispiel das Haarwachstum mehrerer Probanden. Was unser Beispiel dennoch interessant macht: Es kann Ausreißer geben, und mit einer simplen Durchschnittsrechnung würden Sie diesen nicht gerecht werdenMathematische Grundlagen
Sie erinnern sich an den Aufbau einer einfachen linearen Gleichung:f(x) = mx + b
Sie beschreibt eine Gerade mit der Steigung m und dem y-Achsenabschnitt b. Ziel ist es nun also, für m und b Werte zu finden, sodass eine Gerade beschrieben wird, die sich im Durchschnitt möglichst nah an mehreren Messpunkten entlangbewegt.Vorausgesetzt, das System, in dem die Messpunkte erfasst wurden, wird nicht drastisch verändert, erhalten Sie mit einer solchen Geraden die gewünschte Möglichkeit, weitere Werte näherungsweise vorherzubestimmen.Und an dieser Stelle geht es los mit der linearen Regression. Übersetzt steckt hinter diesem mathematischen Ausdruck eine Strategie, bei der Sie sich linear an vorhandene Werte angleichen – hence the name. Dabei ist allerdings von vornherein klar, dass eine solche Linie nicht durch alle Punkte gehen kann, und das ist auch nicht das Ziel.Jeder Datenpunkt in Bild 1 lässt sich beschreiben als ein Wertepaar mit einer x- und einer y-Koordinate. Sie können diese ganz einfach als (x, y) beschreiben. Wenn Sie sich nun eine Linie ausdenken, die sich ungefähr an dem Trend dieser Wertepaare entlangbewegt, dann können Sie erkennen, dass es zu jeder x-Koordinate Ihrer Wertepaare eine neue y-Koordinate gibt, die auf der Linie selbst liegt.Tatsächlich finden Sie in Excel-Arbeitsblättern dazu sogar eine Funktion, die solche Trendlinien beschreibt, und raten Sie mal: Lineare Regression ist das, was sich mathematisch dahinter abspielt. Nur wird diese neue y-Koordinate, nennen Sie sie y', meist unterhalb oder oberhalb Ihrer tatsächlichen y-Koordinate liegen.Dabei handelt es sich also um einen Fehler, wenn Sie so wollen, und um diesen zu beschreiben, benötigen Sie eine Fehler-Funktion.In der Mathematik möchte alles, wirklich alles, mit Funktionen beschrieben werden. Und um dieser Voraussetzung Genüge zu tun, nehmen Sie für den Moment einfach einmal an, dass Sie den Abstand zwischen ihren y-Koordinaten und den entsprechenden Punkten auf der gedachten Linie wie folgt beschreiben:
ε(y, y')
Da Sie nun eine Funktion haben, die den Fehler eines Wertepaares beschreibt, kennen Sie auch das mathematisch formulierte Ziel: Finden Sie eine Funktion f(x) = mx + b, die die Summe aller Fehler minimiert (ohne es dabei zu übertreiben).Dazu muss diese Fehlerfunktion einige Kriterien erfüllen:
- Sie sollte 0 sein für alle y.
- Sie sollte positiv sein.
- Sie sollte symmetrisch sein.
ε(y, y') = ε(y - y')<sup>2</sup>
Und diese gilt es zu minimieren.Sobald Sie sich im Internet mit noch mehr Material zu diesem Thema beschäftigen, werden Sie auf den Begriff Least Square Method treffen – oder auf Deutsch: Die Methode der kleinsten Quadrate. Und das ist es genau, was diese Formel beschreibt.Bildlich können Sie sich das vorstellen wie in Bild 2. Nun können Sie die Forderung von oben auch mathematisch beschreiben.
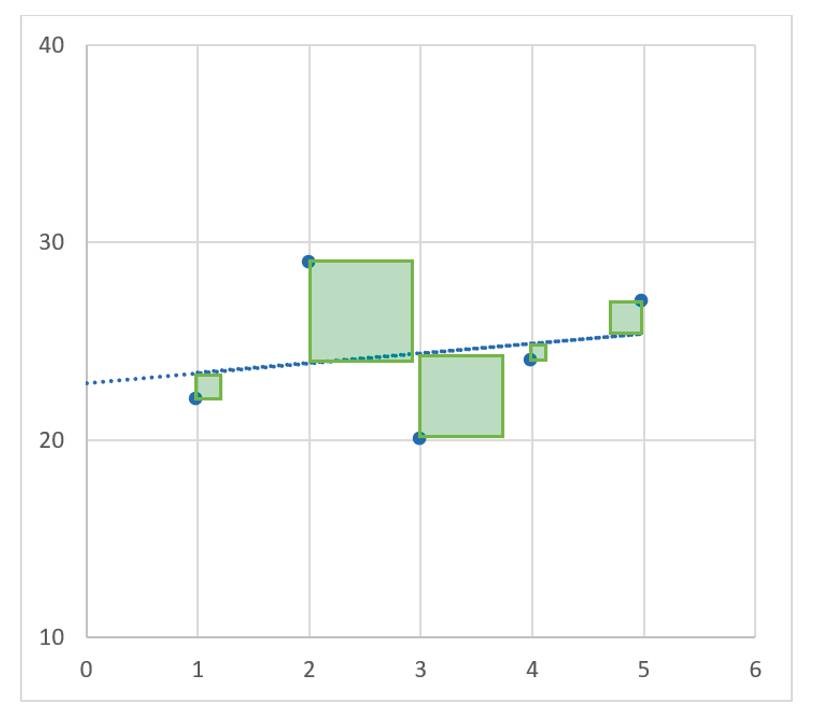
Die Fehlerfunktionzu den Werten aus Tabelle 1(Bild 2)
Autor
Der Teil nach dem Komma in der Fehlerfunktion auf der rechten Seite ist die Abbildung einer jeden y-Koordinate, so wie sie oben beschrieben wird (y').Der Gesamtfehler E wird also auf der Grundlage der Steigung m einer linearen Funktion und ihres y-Achsenabschnittes b berechnet. Die Formel dazu kennen Sie hiermit, und nun gilt es, sie so aufzulösen, dass Sie auch die Forderung, für m und b Werte zu finden, die den Fehler minimieren, mathematisch ausdrücken können.Um bei dem Bild von vorhin zu bleiben, möchten Sie, dass die Fläche der Quadrate (Bild 3) möglichst klein wird.
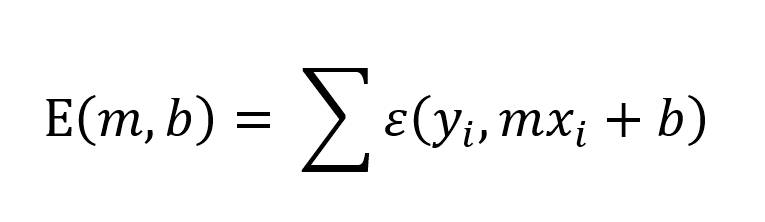
Autor
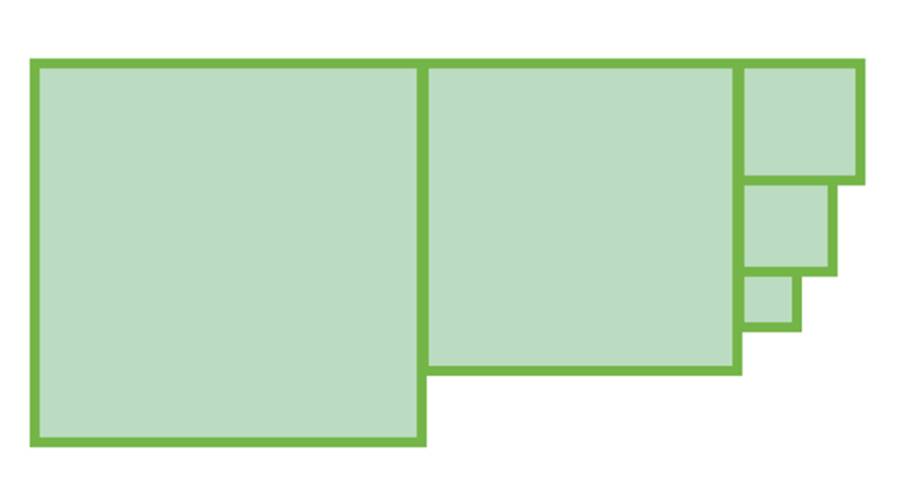
Die Flächeder Quadrate soll minimiert werden(Bild 3)
Autor
Mit der Fehlerfunktion von oben können Sie den Gesamtfehler (Total Error) entsprechend umformulieren:
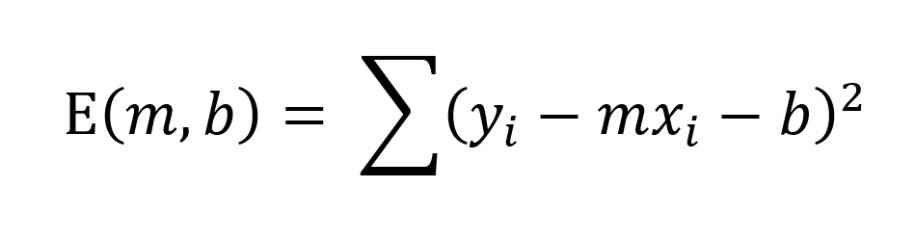
Autor
Ab jetzt wird alles ganz einfach, da es im Grunde genommen nur noch darum geht, eine Gleichung aufzulösen respektive umzuformen.
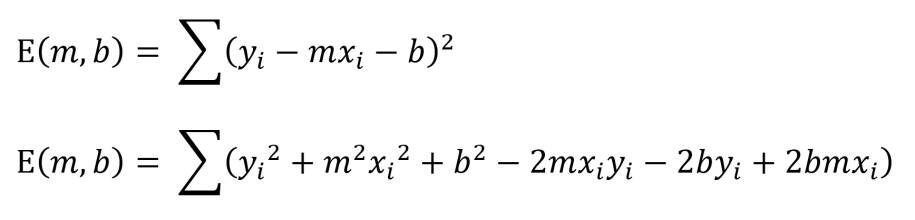
Autor
Für die folgenden Schritte ist es erforderlich, die Summe auseinanderzunehmen und in einzelne Terme zu zerlegen:
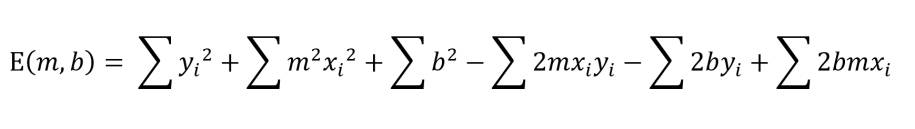
Autor
Da es sich bei m und b um Konstanten handelt, können diese aus den Summen herausgezogen werden:
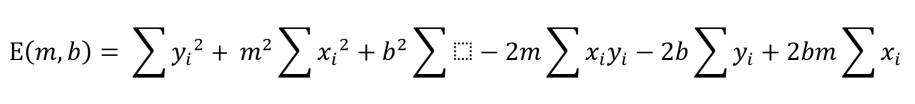
Autor
An dritter Stelle steht nun b2 multipliziert mit der Summe – ja von was eigentlich? Ausgeschrieben müsste es lauten: Die Summe aller xi für i = 0 bis n, wobei n der Anzahl aller Werte entspricht. Werden daher in einem Einzelterm keine Werte mehr aufsummiert, bleibt nur noch die Anzahl aller Wertepaare übrig.
Overfitting
Berechnet man eine Funktion, bei der das Ergebnis einen Verlauf beschreibt, der tatsächlich alle Datenpunkte berührt, nennt man das Overfitting. Das mag zunächst einmal interessant ausschauen, erzeugt aber auf der einen Seite eine ziemlich komplexe Formel und verhindert auf der anderen Seite wiederum eine sinnvolle Aussage darüber, wie der Verlauf weitergeht. Daher gilt es, eine solche Situation zu vermeiden.
Substitution
An dieser Stelle lohnt es sich, die Formel zu vereinfachen. In der Mathematik sagen Sie dazu „substituieren“. Sie ersetzen also einzelne Ausdrücke durch Vereinfachungen, um die weiteren Umwandlungen übersichtlicher zu gestalten. Mit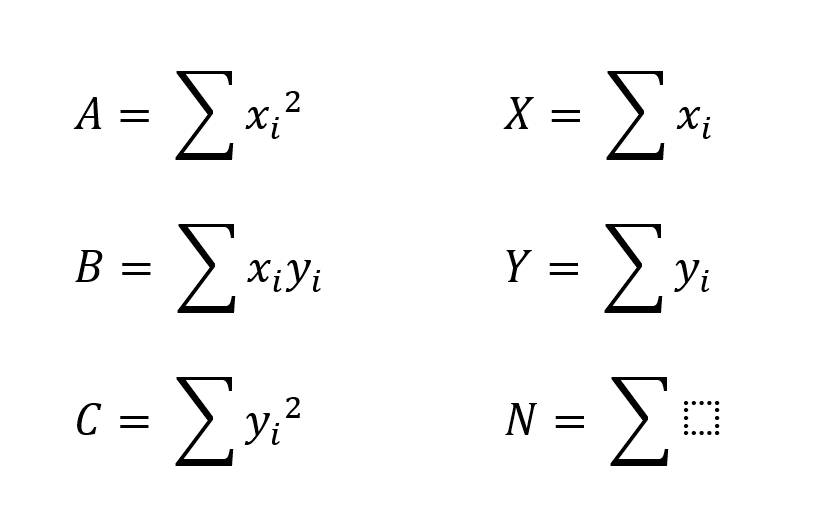
Autor
lässt sich die Formel nun also wie folgt notieren:
E(m,b)= C + m<sup>2</sup>A + b<sup>2</sup>N - 2mB - 2bY + 2bmX
Damit können Sie schon viel leichter arbeiten, oder? Das Ziel ist es nun, mittels dieser Formel die Variablen m und b derart zu bestimmen, dass der Gesamtfehler E minimiert wird. Wie funktioniert das?
Derivation oder Ableitung?
Beide Begriffe beschreiben die gleiche Sache. Allerdings werden Ihnen in der Mathematik oft unterschiedliche Schreibweisen begegnen. In der Schulmathematik finden Sie in der Regel die auch in diesem Artikel genutzte Schreibweise <em>f'(x)</em> und meist wird das auch so simpel ausgesprochen: „F Strich von X“. Und gemeint ist damit die erste Ableitung. In Universitäten wird – ausgehend vom Fachterminus Derivation – meist der griechische Buchstabe Delta verwendet und man spricht in der sogenannten Differentialrechnung von einer partiellen Ableitung. Entsprechend würden Sie Gleichungen vorfinden, in denen öfter mal ein Delta vorkommt und von Derivaten gesprochen wird. Lassen Sie sich davon aber nicht verwirren.
Fehler minimieren
Sie haben nun schon mehrfach den Ausdruck „minimieren“ gehört. Mathematisch ausgedrückt ist damit gemeint, dass Sie etwa in einer Gleichung mit einer Variablen für diese einen Wert finden wollen, der zu dem kleinstmöglichen Ergebnis führt. Erinnern Sie sich an Ihren Mathematikunterricht? Bei einer einfachen quadratischen Gleichungen wie zum Beispiel f(x) = x2 ging es darum, für x einen Wert zu finden, bei dem die Steigung gleich null ist.Da der Graph dieser Gleichung durch den Nullpunkt geht, ist das Beispiel eher witzlos, mathematisch betrachtet aber zeigt es das Vorgehen auf denkbar einfache Weise:Im ersten Schritt bilden Sie aus der Gleichung die erste Ableitung, also ein Derivat. Für f(x) = x2 ist das f'(x) = 2x.Die erste Ableitung einer quadratischen Gleichung entspricht der Steigungsfunktion – sie gibt also die Steigung in einem beliebigen Punkt an.Und diese Gleichung setzen Sie mit null gleich, um den Wert für x zu minimieren. Also 2x = 0. Nach x aufgelöst ergibt sich somit konsequenterweise: x = 0. An diesem Punkt ist die Steigung entsprechend gleich null, Weniger geht nicht. Grundsätzlich.Das gleiche Prinzip wenden Sie auf die obige Fehlerformel an, mit einer kleinen Ergänzung: Da Sie sowohl für m als auch für b entsprechende Werte suchen, die die jeweiligen Ergebnisse der Formel minimieren, teilen Sie die Fehler-Funktion nach m und b auf:E(m) = m<sup>2</sup>A - 2mB + 2bmX
E(b) = b<sup>2</sup>N - 2bY + 2bmX
Nun bilden Sie jeweils die erste Ableitung:
E‘(m)= 2mA - 2B + 2bX
E‘(b)= 2bN - 2Y + 2mX
Und diese beiden Gleichungen setzen Sie jeweils gleich null und lösen Sie auf mittels Termumformung und Einsetzung auf:
mA – B + bX = 0 <em>(a)</em>
b = (Y - mX) / N <em>(b)</em>
Einsetzen von (b) in (a):
mA – B + (Y – mX) X / N = 0
mAN = NB – XY + mX<sup>2</sup>
m = (NB - XY) / (NA- X<sup>2</sup> )
Und damit stehen die Formeln zur Ermittlung von m und b fest. Sie sehen auch, dass es deutlich entspannter war, die Formeln mittels Substitution zu erarbeiten. Was nun abschließend also noch fehlt, ist die Resubstitution. Sie ersetzen also die Platzhalter X, Y, A, B, C und N wieder durch ihre eigentlichen Bedeutungen und erhalten folgende Formeln, mittels derer Sie einfach m und b errechnen.
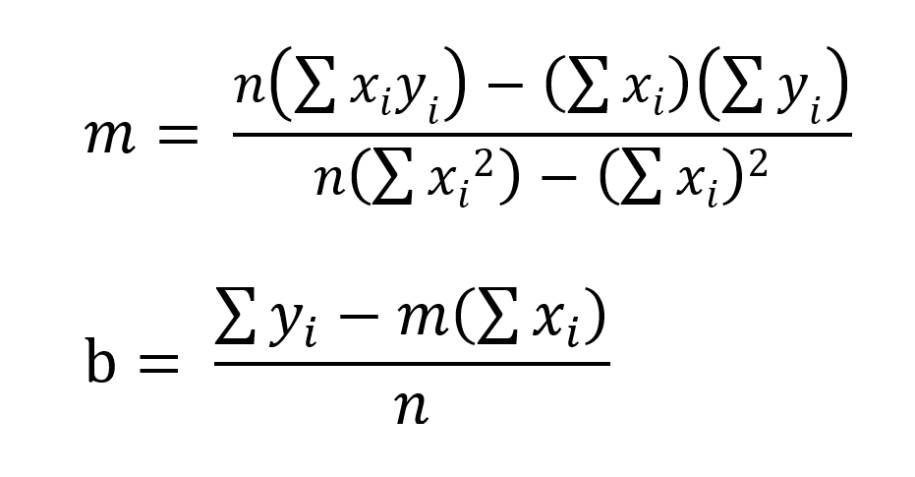
Autor
In unserem Fall nehmen wir nun die Daten aus Tabelle 1, die insgesamt über n = 5 Messpunkte verfügt. In der folgenden erweiterten Tabelle 2 sind die Summen und sonstigen Berechnungen bereits ergänzt.
Tabelle 2: Erweiterte Tabelle 1
|
m = ((5 * 371) - (15 * 122)) / ((5 * 55) - (15)<sup>2</sup> )
m = 25 / 50 = 0,5
b = (122 - 0,5 * 15) / 5 = 22,9
Und daraus ergibt sich:
f(x) = 0,5x + 22,9 Blick in die Glaskugel
Wenn Sie bis hierher alle Schritte nachvollziehen konnten, ist das ein wahrer Meilenstein. Denn obwohl es noch einiges mehr an Mathematik braucht, um heute KI-Modelle zu erzeugen und damit Berechnungen anzustellen, kennen und verstehen Sie nun eine der wesentlichen Grundlagen, auf denen fast alles aufbaut.Um nun bei dem für diesen Artikel gewählten Beispiel zu bleiben, können Sie jetzt die Frage beantworten, wann voraussichtlich für weitere erfolgreiche Geschäfte das entsprechende Verbrauchsmaterial nachbestellt werden sollte.Falls Sie dafür auch auf einen Zeitpunkt circa 26 Tage im Anschluss an die letzte Bestellung kommen, lägen Sie richtig! Sogar Excel bekommt das hin (Bild 4).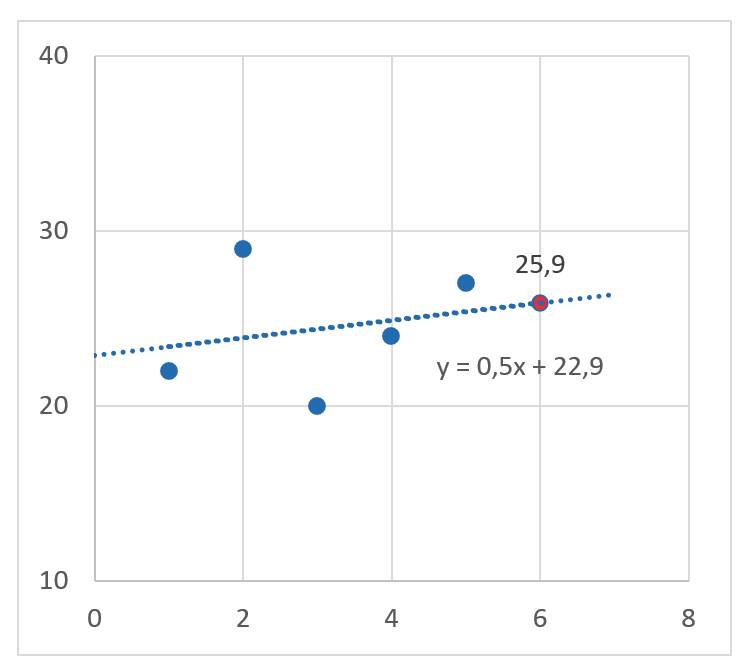
Die interpolierte Geradezeigt den nächsten Bestellzeitpunkt an(Bild 4)
Autor