18. Nov 2024
Lesedauer 10 Min.
Knoten- und Kantenkunde
C#-Graphen-Algorithmen
Ein Programmbeispiel zeigt, wie Sie Graphen-Algorithmen für die Tiefen- und die Breitensuche in C# entwickeln.
dotnetpro
Graphen-Algorithmen spielen in der heutigen Softwareentwicklung eine entscheidende Rolle. So liefern sie Antworten auf komplexe Fragestellungen in der Routenplanung, in Kommunikations-, Vertriebs- und Versorgungsnetzwerken sowie in Such- und Optimierungsverfahren.Ein Graph ist hierbei ein abstraktes mathematisches Konstrukt, das als Werkzeug zur Modellierung von strukturellen Zusammenhängen verwendet wird.Der Graph besteht aus Knoten (englisch: Vertices), die durch Kanten (englisch: Edges) miteinander verbunden sein können. Konkret ist ein Knoten (Vertex) in der grafischen Darstellung ein Punkt, und die Kante (Edge) ist eine Linie, die zwei Knoten verbindet. Bild 1 zeigt beispielhaft die Bahnverbindung mit Städten in Deutschland als Graphenmodell.
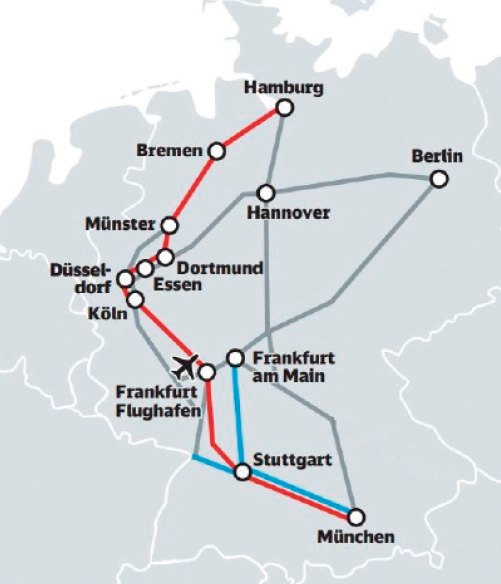
Bahnverbindungen in Deutschland (Bild 1)
Autor
Der Umgang mit einem solchen Modell ist ein wichtiges Hilfsmittel in der Informatik. Einige der Anwendungsfälle von Graphen sind:
- Routenplanung: Ein klassisches Problem der Graphentheorie. Hier repräsentieren die Knoten wichtige Orte, die Kanten stellen verbindende Straßen dar.
- Kürzeste Wege: Hier werden Graphen für die Darstellung von Infrastruktur- und Kommunikationsnetzen genutzt, um den Weg zwischen zwei gegebenen Knoten zu ermitteln. Hierbei kann es sich um den kürzesten Weg oder aber auch um den schnellsten Weg handeln. Auch Wege mit dem geringsten Energieverbrauch, den geringsten Kosten und anderen Optimierungen können bestimmt werden.
- Matchings: Das Matching-Problem fragt nach einer Zuordnung zwischen Elementen von verschiedenen Mengen. Ein Matching besteht dann in der Bildung von Paaren, die alle miteinander übereinstimmend sind.
- Flüsse: Hierbei handelt es sich um die Problemstellung, einen Fluss (Güter-, Kommunikation-, Transport- oder Versorgungsfluss) zu bestimmen. Meist ist das Ziel, einen maximalen Fluss zwischen zwei gegebenen Knoten zu ermitteln, wobei die Kapazität jeder einzelnen Kante beschränkt ist.
Graphen-Datenstruktur
Auch im Programmcode stellt ein Graph eine nichtlineare Datenstruktur dar, die aus Knoten und Kanten besteht. Kanten sind hierbei immer Linien oder Bögen, die zwei beliebige Knoten in einem Graphen miteinander verbinden. Knoten werden auch als Scheitelpunkte bezeichnet. Somit besteht ein Graph aus einer endlichen Anzahl an Knoten und einer Reihe von Kanten, die sie verbinden.Bild 2 zeigt einen ungerichteten Graphen ohne Mehrfachkanten. Dargestellt ist dort die Menge der Knoten (Vertices) V={A,B,C,D,E} und die Menge der Kanten (Edges) E={AB,AC, AD,BD,BE,CD,DE}.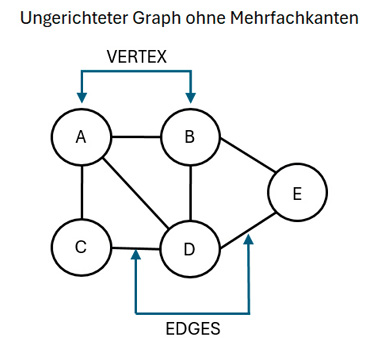
Ungerichteter Graph ohne Mehrfachkanten (Bild 2)
Autor
Es gibt verschiedene Arten von Graphen, deren jeweilige Eigenschaften und Besonderheiten auf der Position dieser Knoten und Kanten basieren. Die wichtigsten sind:
- Digraphen: Man unterscheidet ungerichtete Graphen (Bild 2) von gerichteten Graphen (Bild 3), bei denen Kanten nur in der angegebenen Richtung durchlaufen werden dürfen. Diese Graphen werden als Digraph (Directed Graph) bezeichnet.
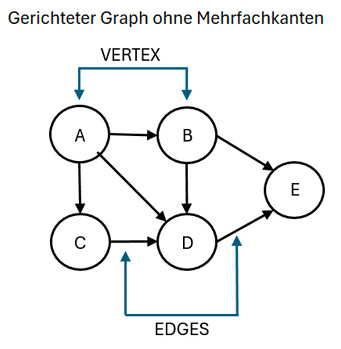
Gerichteter Graph ohne Mehrfachkanten (Bild 3)
Autor
- Multigraphen: Ein Multigraph ist ein ungerichteter Graph, der zahlreiche Kanten zulässt. Zwei oder mehr Kanten, die dieselben zwei Knoten verbinden, sind sogenannte Mehrfachkanten. Normalerweise gibt es zwischen zwei Knoten maximal eine Kante.
- Gewichteter Graph: In einem gewichteten Graphen bekommt jede Kante noch eine Zusatzinformation, das Gewicht. Dieses Gewicht kann zum Beispiel die Länge der Kante darstellen. Es ist aber auch möglich, über das Gewicht anzugeben, wie viele Kanten zwischen zwei Knoten existieren.
- Teilgraph: Ein Teilgraph ist eine Teilmenge der Knotenmenge und der Kantenmenge innerhalb eines Graphen.
- Vollständiger Graph: In einem vollständigen Graphen ist jeder Knoten mit jedem anderen Knoten durch genau eine Kante verbunden.
- Getrennter Graph: Wenn mindestens zwei der Knoten des Graphen nicht durch eine Kante verbunden sind, bezeichnet man den Graphen als unzusammenhängend.
- Zyklenfreier Graph: Ein Zyklus beschreibt den geschlossenen Kantenzug in einem Graphen. Kommt im Zyklus jeder Knoten maximal einmal vor, dann bezeichnet man den Zyklus als Kreis. Graphen ohne Zyklen heißen zyklenfrei oder azyklisch. Ein zyklusfreier, zusammenhängender Graph ist immer ein Baum.
Graphenterminologie
Für die Entwicklung eines Graph-Algorithmus müssen als Erstes die Begrifflichkeiten der Graphdatenstruktur bestimmt werden:- Kanten sind die grundlegenden Elemente, aus denen Graphen aufgebaut sind. Hierbei hat jede Kante zwei Enden, mit denen sie verbunden ist.
- Wenn zwei Eckpunkte Endpunkte derselben Kante sind, sind sie benachbart.
- Die ausgehenden Kanten eines Knotens (Scheitelpunkts) sind gerichtete Kanten, bei denen der Knoten der Ursprung ist.
- Die eingehenden Kanten eines Knotens sind gerichtete Kanten mit dem Knoten als Ziel.
- Die Anzahl der Kanten, die zu einem Knoten in einem Diagramm gehören, entspricht seinem Grad.
- Jede Kante hat zwei Enden, die sogenannten Scheitelpunkte, mit denen sie verbunden ist.
- Ein Zyklus ist definiert als eine Reise, die gleichzeitig beginnt und endet.
- Ein Pfad mit eindeutigen Scheitelpunkten wird als einfacher Pfad bezeichnet.
- Ein Graphdiagramm, das keine Zyklen aufweist, wird als Wald bezeichnet.
- Ein Baum ist ein verknüpfter Graph, der keine Zyklen hat. Wenn alle Zyklen in einem Directed Graph entfernt werden, wird er zu einem Baum, und wenn eine Kante in einem Baum entfernt wird, wird er zu einem Wald.
Darstellung von Graphen
Zwei wichtige Darstellungsformen von Graphen sind die Adjazenzmatrix und die Adjazenzliste. Bei der Darstellung als Adjazenzmatrix wird eine Matrixstruktur verwendet, um einen Graphen repräsentieren. Die Zeilen- und Spaltenindikatoren stehen für die Knoten und die Werte in jeder Zelle für die Kanten. Der Wert einer Zelle wird als 1 markiert, wenn es eine Kante zwischen zwei Knoten gibt, andernfalls wird dieser mit 0 markiert.In der Adjazenzlisten-Darstellung wird eine Array-Struktur verwendet, um einen Graphen dazustellen. Bild 4 zeigt die Darstellung eines ungerichteten Graphen sowohl als Matrix wie auch als Liste.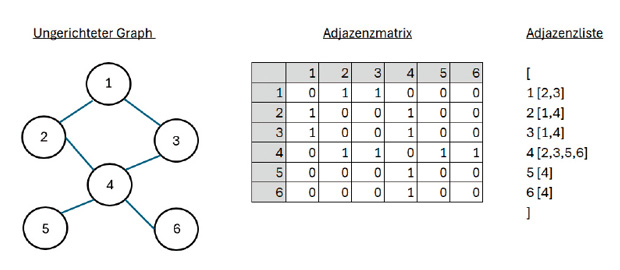
Ungerichteter Graph als Adjazenzmatrix und -liste (Bild 4)
Autor
Beide Darstellungen haben ihre eigenen Vor- und Nachteile. Wenn Sie insgesamt V Knoten und E Kanten haben, sollte der Null(0)-Vergleich aus Bild 5 eine Vorstellung davon vermitteln, welche Darstellung zu verwenden ist.
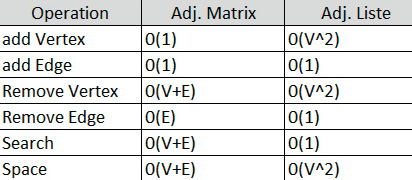
Vor- und Nachteile bei der Berechnung (Bild 5)
Autor
Die Adjazenzliste verbraucht weniger Arbeitsspeicher und ist schneller darin, alle Kanten zu finden und zu iterieren; allerdings ist sie langsamer, um eine Kante zwischen zwei Eckpunkten zu finden.Die Adjazenzmatrix verbraucht mehr Speicher und ist langsamer dabei, alle Kanten zu finden und darüber zu iterieren; allerdings gelingt es mit ihr schneller, eine Kante zwischen zwei Scheitelpunkten zu finden.So weit die theoretische Einführung. Sie können nun mit der Implementierung eines Graphen mithilfe einer Adjazenzliste beginnen. Mehr theoretisches Wissen über Graphen finden Sie unter [1].
Die Aufgabe
Mit Ihrem jetzigen Wissen über die Graphdatenstruktur können Sie ohne weitere Umwege in das Beispiel einsteigen. Die Aufgabenstellung ist im Bild 6 abgebildet: Es geht um das Durchlaufen der Datenstruktur eines Graphen, bei dem es noch keine eindeutige Identifizierung der untergeordneten Ebenen gibt.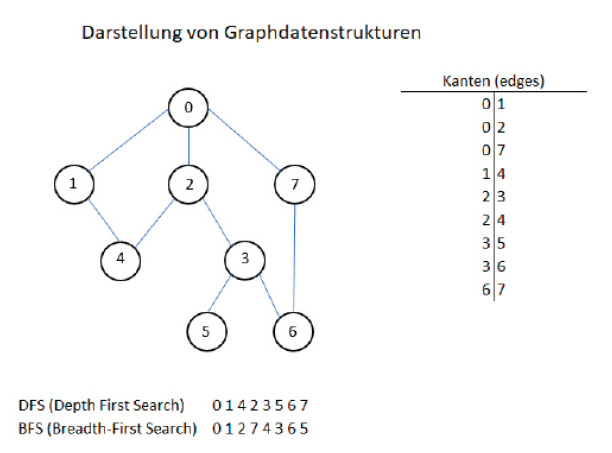
Aufgabenstellung zum Durchlaufen des Graphen (Bild 6)
Autor
Um die Datenstruktur eines solchen Graphen zu erschließen, werden zunächst alle Scheitelpunkte im Graphen identifiziert, indem sie besucht werden; dieser Vorgang wird als Graph Traversal bezeichnet. Das Graph Traversal findet im Suchprozess auch die verwendeten Kanten und verwendet dabei Verfahren, die keine Schleifendurchläufe erzeugen, um den Suchprozess möglichst kurz zu halten. Dazu ist es erforderlich, bereits besuchte Scheitelpunkte als solche zu kennzeichnen, um sie nicht häufiger als nötig anzusteuern.Das Graph Traversal nutzt im Wesentlichen zwei Algorithmen zum Durchlaufen von Graphen, die sich in der Reihenfolge unterscheiden, in der die Knoten besucht werden: Depth First Search (DFS) und Breadth First Search (BFS).
Depth First Search (DFS)
Der Depth-First-Search-Algorithmus wird auch als Tiefensuche bezeichnet. Die Tiefensuche stellt einen rekursiven Algorithmus zum Erfassen aller Knoten eines Graphen oder einer Baumdatenstruktur zur Verfügung. Bei der Durchquerung des Graphen werden alle Knoten besucht.Die Standard-Implementierung ordnet jeden Scheitelpunkt des Graphen einer von zwei Kategorien zu: „besucht“ und „nicht besucht“. Die angestrebte Lösung des Algorithmus besteht darin, jeden Knoten als besucht zu markieren und gleichzeitig Zyklen zu vermeiden.Der Depth-First-Search-Algorithmus durchläuft folgende Schritte:- Schritt 1: Legen Sie einen beliebigen Knoten des Graphen auf einen Stapel.
- Schritt 2: Nehmen Sie das oberste Element des Stapels und fügen Sie es der Liste der besuchten Elemente hinzu.
- Schritt 3: Erstellen Sie eine Liste der benachbarten Knoten dieses Scheitelpunkts. Fügen Sie diejenigen, die nicht in der besuchten Liste enthalten sind, oben im Stapel hinzu.
- Schritt 4: Wiederholen Sie die Schritte 2 und 3, bis der Stapel leer ist.
- Schritt 5: Wenn der Stapel leer ist, erstellen Sie den endgültigen Spannbaum (Spanning Tree) [2], indem Sie die nicht verwendeten Kanten des Graphen löschen.
Listing 1: Pseudocode für Depth First Search
<span class="hljs-function"><span class="hljs-title">DFS</span><span class="hljs-params">(G, u)</span></span><br/> u<span class="hljs-selector-class">.besucht</span> = wahr<br/> für jedes v G<span class="hljs-selector-class">.Adj</span>[u]<br/> wenn v<span class="hljs-selector-class">.besucht</span> == false<br/> DFS(G,v)<br/> <br/>init() {<br/> Für jedes u G<br/> u<span class="hljs-selector-class">.besucht</span> = false<br/> Für jedes u G<br/> DFS(G, u)<br/>}
Der Depth-First-Search-Algorithmus findet in folgenden Anwendungen Verwendung:
- Um Wege im Graphen zu finden.
- Zum Testen, ob es sich um einen Bipartiter-Graphen [3] handelt.
- Zum Finden stark verbundener Komponenten eines Graphen.
- Zur Erkennung von Zyklen in einem Diagramm.
Breadth First Search (BFS)
Auch bei diesem Algorithmus sorgt die Traversierung dafür, dass alle Knoten eines Graphen besucht werden. Die angewandte Breitensuche ist ein rekursiver Algorithmus zum Durchsuchen aller Knoten eines Graphen oder einer Baumdatenstruktur.Die Standardimplementierung des Breadth-First-Search-Algorithmus ordnet jeden Scheitelpunkt des Graphen den Kategorien „besucht“ oder „nicht besucht“ zu. Die Umsetzung des Breadth-First-Search-Traversals erfolgt in folgenden Schritten:- Schritt 1: Legen Sie einen beliebigen Knoten des Graphen an das Ende einer Warteschlange.
- Schritt 2: Nehmen Sie das vordere Element der Warteschlange und fügen Sie es der besuchten Liste hinzu.
- Schritt 3: Erstellen Sie eine Liste der benachbarten Knoten dieses Scheitelpunkts. Fügen Sie diejenigen, die nicht in der besuchten Liste enthalten sind, am Ende der Warteschlange hinzu.
- Schritt 4: Wiederholen Sie die Schritte 2 und 3, bis die Warteschlange leer ist.
- Schritt 5: Da die Warteschlange leer ist, ist die Breitensuche des Graphen abgeschlossen.
Listing 2: Pseudocode für Breadth First Search
eine Warteschlange erstellen Q<br/>v als besucht markieren und v in Q einfügen<br/>während Q nicht leer ist<br/> entferne den Kopf u von Q<br/> markiere und stelle alle (nicht besuchten) <br/> Nachbarn von u in die Warteschlange
Der Breadth-First-Search-Algorithmus kann für folgende Bereiche verwendet werden:
- Erstellen eines Index anhand des Suchindexes,
- GPS-Navigation,
- Pfadfindungsalgorithmen,
- im Ford-Fulkerson-Algorithmus [4] zum Finden des maximalen Flusses in einem Netzwerk,
- Zyklenerkennung in einem ungerichteten Graphen sowie
- im minimalen Spannbaum [2].
Implementierung in C#
Zur Erstellung dieses Programmbeispiels wird als Entwicklungsumgebung Visual Studio 2022 (in einer Version ab Community Edition) mit dem .NET Framework 8.0 verwendet. Alternativ können Sie auch .NET Framework 6.0 benutzen.Legen Sie für das Beispiel ein neues Console-App-Projekt in Visual Studio an. Vergeben Sie als Project name den Begriff GraphenAlgorithmus und wählen Sie .NET 8.0 als Framework aus. Nach dem Klick auf die Schaltfläche Create erstellt Visual Studio automatisch ein lauffähiges Konsolenprogramm mit der Ausgabe Hello World!Im nächsten Schritt können Sie für das Beispiel die beiden Codezeilen in der Klasse Program.cs entfernen.Im Beispiel soll der Graph aus Bild 6 durchlaufen werden, um die beiden Algorithmen Depth First Search und Breadth First Search auszuführen. Die Angaben zum Kantenverlauf und die Ergebnisse der Spannbäume sind entsprechend aufgeführt.Der Programmcode in Listing 3 ist die Hauptmethode, mit der Sie die Algorithmen-Traversierung eines Graphen auf der Konsole ausgeben können. Bei der ersten Tiefensuche (DFS) beginnen Sie mit einem Knoten und durchlaufen einen Zweig, wobei alle Knoten abgedeckt werden, bevor Sie zum nächsten Zweig kommen. Es kann verschiedene Varianten geben, die auf Pre Order, In Order oder Post Order basieren.Listing 3: Implementierung der Algorithmen
using System.Threading;<br/>int vx = 8;<br/>int e = 9;<br/>int[] vertex = new int[vx];<br/>int[,] edges = new int[vx, vx];<br/>bool[] visited = new bool[vx];<br/>Console.WriteLine("Enter Kantenverbindungen");<br/>for (int i = 0; i &lt; e; i++)<br/>{<br/> int s, d;<br/> string[] input = Console.ReadLine().Split(' ');<br/> int.TryParse(input[0], out s);<br/> int.TryParse(input[1], out d);<br/> edges[s, d] = 1;<br/> edges[d, s] = 1;<br/>}<br/>Console.WriteLine(<br/> "Ausgabe Depth First Search Algorithmus");<br/>for (int i = 0; i &lt; vx; i++)<br/>{<br/> if (!visited[i])<br/> DepthFirstSearch(edges, vx, visited, i);<br/>}<br/>for (int i = 0; i &lt; vx; i++)<br/>{<br/> visited[i] = false;<br/>}<br/>Console.WriteLine();<br/>Console.WriteLine(<br/> "Ausgabe Breadth First Search Algorithmus");<br/>for (int i = 0; i &lt; vx; i++)<br/>{<br/> if (!visited[i])<br/> BreadthFirstSearch(edges, vx, visited, i);<br/>}<br/>Console.ReadLine();<br/>static void DepthFirstSearch(int[,] edges, int v, <br/> bool[] visited, int si)<br/>{<br/> visited[si] = true;<br/> Console.Write(si + " ");<br/> for (int i = 0; i &lt; v; i++)<br/> {<br/> if (i == si)<br/> continue;<br/> if (!visited[i] &amp;&amp; edges[si, i] == 1)<br/> {<br/> DepthFirstSearch(edges, v, visited, i);<br/> }<br/> }<br/>}<br/>static void BreadthFirstSearch(int[,] edges, int v, <br/> bool[] visited, int si)<br/>{<br/> Queue&lt;int&gt; queue = new Queue&lt;int&gt;();<br/> queue.Enqueue(si);<br/> visited[si] = true;<br/> while (queue.Count != 0)<br/> {<br/> int currentVertex = queue.Dequeue();<br/> Console.Write(currentVertex + " ");<br/> for (int i = 0; i &lt; v; i++)<br/> {<br/> if (i == currentVertex)<br/> continue;<br/> if (!visited[i] &amp;&amp; edges[currentVertex, i] == 1)<br/> {<br/> queue.Enqueue(i);<br/> visited[i] = true;<br/> }<br/> }<br/> }<br/>}
Der Code aus Listing 3 zeigt zunächst die Depth-First-Search-Traversierung des Graphen. Die Variablen vx = 8 und e = 9 geben die Knoten- und Kanten-Anzahl für den Graphen aus Bild 6 wieder. Die Variablen vertex, edges und visited speichern die Kanten des Graphen, alle Knoten und besuchte Knoten.Die erste for-Schleife dient zur Eingabe der Kantenverbindung. Danach beginnen Sie mit einem Knoten, der mit der Variablen i (si) an die Methode DepthFirstSearch(...) übergeben wird. Die for-Schleife iteriert über jeden Scheitelpunkt und markiert jeden besuchten Knoten. Außerdem wird für jeden Knoten rekursiv die DepthFirstSearch-Methode aufgerufen.Bei der anschließenden Breitensuche im Breadth-First-Search-Algorithmus werden zunächst alle Knoten auf derselben Ebene oder in derselben Tiefe durchsucht, bevor die nächste Ebene erreicht wird. Im Beispiel wird die Warteschlange aus der .NET-Klasse Queue zum Speichern aller Kanten desjenigen Knotens genutzt, der gerade iteriert wird. Die Methode Enqueue fügt am Ende der Warteschlange (Queue) ein Element hinzu. Dequeue entfernt das älteste Element vom Anfang der Queue.Bild 7 zeigt das lauffähige Programmbeispiel mit der entsprechenden Ausgabe der Tiefen- und Breitensuche.
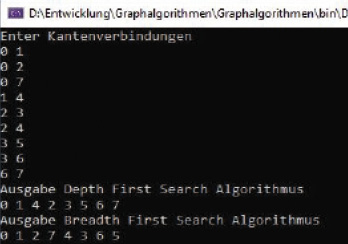
Die beiden Algorithmen im Test (Bild 7)
Autor
Fazit
Dieser kleine Workshop sollte aufzeigen, welche Anwendungen von Graphen im Alltag eine Rolle spielen. Ob es sich dabei um Netzwerke, Landkarten oder um das soziale Netzwerk handelt – in diesem stellt die Person den Knoten dar und die Kanten die Verbindung zu Freunden –, überall trifft man auf Graphen.Des Weiteren sollte aufgezeigt werden, wie man aus einer formal aufgezeigten Terminologie selbstständig einen Algorithmus für die Tiefen- und Breitensuche entwickeln kann.Werfen Sie doch einfach mal einen Blick auf weitere Graphen-Algorithmen wie Dijkstra [5] und Jarník [6] und erweitern Sie den Programmcode beziehungsweise die Algorithmen nach Belieben weiter, um zum Beispiel mit Gewichten in Graphen zu arbeiten. Für Sie als Entwickler bleibt das Thema Graphen auf jeden Fall spannend.Fussnoten
- Graphentheorie, http://www.dotnetpro.de/SL2412Graphen1
- Spannbaum bei Wikipedia, http://www.dotnetpro.de/SL2412Graphen2
- Bipartiter Graph bei Wikipedia, http://www.dotnetpro.de/SL2412Graphen3
- Algorithmus von Ford und Fulkerson bei Wikipedia, http://www.dotnetpro.de/SL2412Graphen4
- Dijkstra-Algorithmus bei Wikipedia, http://www.dotnetpro.de/SL2412Graphen5
- Jarník bei Wikipedia, http://www.dotnetpro.de/SL2412Graphen6
