Mathematik mit .NET
Best of NuGet, Teil 3

Gleich zur Einleitung sei angemerkt, dass es unter dem Begriff Math.NET eine ganze Gruppe von Bibliotheken zu besprechen gibt. Die Webseite des Projekts präsentiert sich wie in Bild 1 gezeigt.
Angemerkt sei außerdem, dass dieser Artikel grundlegende Kenntnisse im Bereich der Ingenieurmathematik voraussetzt. Wer keine Kompetenz im Bereich der Mathematik mitbringt, wird bei der Nutzung Probleme bekommen – ein Faktum, das sich das Ökosystem allerdings zum Beispiel auch mit Kryptografie-Bibliotheken teilt.

Ähnlichkeiten zur Aufteilung einer Mathematik-Fakultät sind rein zufällig (Bild 1)
AutorAuch für F#
Insbesondere im Bereich der Algorithmen-Simulation erfreut sich F# großer Popularität. Math.NET unterstützt auch diese Sprache. Schon im Interesse der einfacheren Zugänglichkeit werden wir jedoch in den folgenden Schritten mit C# arbeiten.
Von Vektor und Gleichung
Im Bereich der Numerik erfolgt ein Gutteil der Operationen mit in Matrizen vorliegenden Elementen. Als erstes Demonstrationsbeispiel wollen wir eine Konsolenapplikation ins Leben rufen, die das NuGet-Paket MathNet.Numerics eingeschrieben bekommt. Auch das Math.NET-Entwicklerteam unterteilt seine Bibliothek im Interesse der optimalen Speicherplatzausnutzung in mehrere Untergruppen, um uns das Mitschleppen von nicht benötigten Bibliotheken in der Applikation zu ersparen.
Wie bei so gut wie alle anderen Mathematikbibliotheken gilt, dass auch Math.NET verschiedene hauseigene Matrixrepräsentationsklassen zur Verfügung stellt. Von besonderer Wichtigkeit ist der Unterschied zwischen Dense- und Sparse-Matrizen: Eine Dense-Matrix ist im Prinzip ein gewöhnliches Array, während eine Sparse-Matrix bei der Verarbeitung von Feldern, die extrem viele 0-Werte aufweist, eine wesentlich bessere Performance liefert. Für die Erzeugung stehen Abkürzungsmethoden zur Verfügung, die sich nach folgendem Schema einsetzen lassen:
var M = Matrix<double>.Build; var V = Vector<double>.Build; var m = M.Random(3, 4); var v = V.Dense(10);
Ein weiterer interessanter Aspekt ist die Konstantenbibliothek, die viele gerne und häufig verwendete numerische Konstanten – beispielsweise in Algorithmen – direkt ansprechbar macht. Bei Nutzung ist unbedingt ein explizites Using-Statement erforderlich, weil es im Visual Basic nämlich bereits eine ähnliche Bibliothek gibt:
using MathNet.Numerics; Console.WriteLine(Constants.Avogadro);
Lösen linearer Gleichungssysteme mit Math.NET
Das Traktieren von Schülern und Abiturienten mit der manuellen Lösung von linearen Gleichungssystemen ist insbesondere bei kleinen Systemen inklusive 3 × 3 unnötig. Mit dem Matrix- beziehungsweise Determinantenverfahren steht ein numerischer Prozess zur Verfügung, der – solange der manuelle Lösungsweg nicht Teil der Anforderungen ist – die Erledigung der meisten Schularbeiten wesentlich erleichtert.
Angesichts der immensen Verbreitung linearer Gleichungssysteme gibt es in Math.NET natürlich ein dafür vorgesehenes Feature. Zu seiner Illustration wollen wir die in Bild 2 gezeigte Gleichung auswerten, die vom Entwicklerteam als Beispiel zur Verfügung gestellt wird.
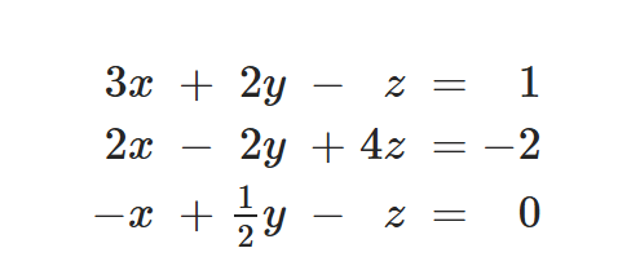
Diese Gleichung dient als Testkandidat (Bild 2)
AutorAnalog zur Arbeit auf dem Papier gilt auch im Fall von Math.NET, dass im ersten Schritt die beiden Matrizen in Form der Vektor-Elemente vorliegen müssen:
using MathNet.Numerics.LinearAlgebra;
var A = Matrix<double>.Build.DenseOfArray(new double[,] {
{ 3, 2, -1 },
{ 2, -2, 4 },
{ -1, 0.5, -1 }
});
var b = Vector<double>.Build.Dense(new double[] { 1, -2, 0 });
Die eigentliche Auflösung des gleichen Systems erfolgt dann mit einem einzigen Befehl:
var x = A.Solve(b); Console.WriteLine(x.ToString());
Als Ergebnis der Programmausführung erscheint das in Bild 3 gezeigte Fenster.
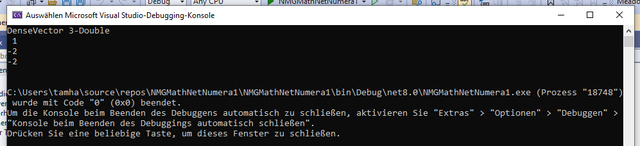
Die Lösung des Linear-Gleichungssystems verlief erfolgreich (Bild 3)
AutorExkurs: Generierung von Zufallszahlen
Bevor wir uns der symbolischen – der Mathematiker versteht darunter die Arbeit mit Variablen – Variante der Bibliothek zuwenden, sei noch ein kurzer Exkurs in die Welt der Monte-Carlo-Umgebungen erlaubt. Dabei handelt es sich um ein Programmierverfahren, das sich auch im täglichen Leben zur Lösung verschiedenster Fragen gewinnbringend heranziehen lässt (zum Beispiel: Kaufe ich das langlebige, aber teure Produkt?). Zum Verständnis bietet sich die Ermittlung der Kreiszahl Pi an, die über das in der Bild 4 gezeigte Objekt erfolgt.
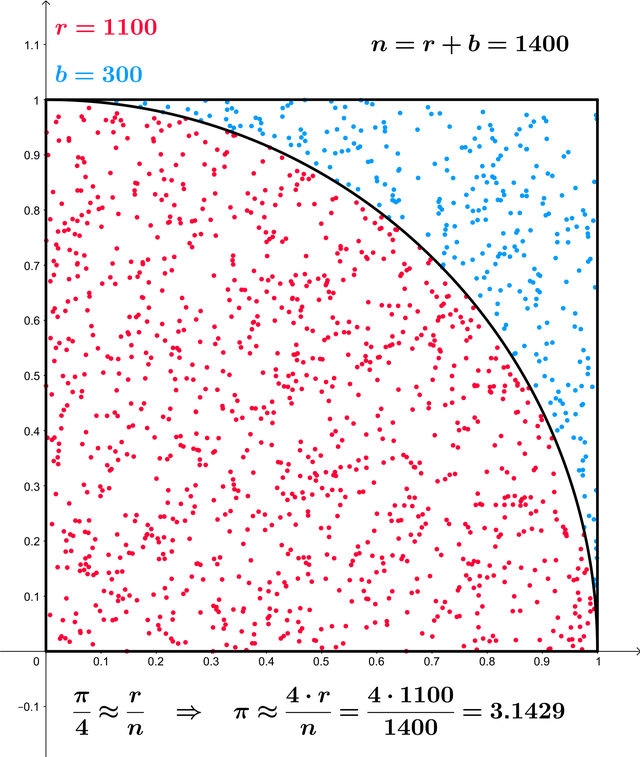
Diese Vorlage hilft bei der Monte-Carlo-basierten Ermittlung der Kreiszahl (Bild 4)
Wikimedia Commons/KmhkmhTrick ist, dass man bei einem beliebigen Koordinatenpaar x | y einfach feststellen kann, ob es „innerhalb“ oder „außerhalb“ des Kreises zu liegen kommt. Die Ermittlung der Kreiszahl erfolgt dann durch permanentes Beschießen dieses Objekts mit unendlich vielen zufällig ausgewählten Punkten. Die Applikationslogik zählt permanent mit, wie viele der Punkte innerhalb und wie viele außerhalb zu liegen kommen. Aus dieser Funktionsbeschreibung folgt, dass die erfolgreiche Ausführung einer Monte-Carlo-Umgebung Zufallszahlen hoher Qualität voraussetzt – spezifischerweise Zufallszahlen, die gleichmäßig über den gesamten Zahlenbereich des Generators verteilt sind.
Insbesondere im Bereich der Kryptografie – ein Thema, das wir hier nicht weiter vertiefen werden – gibt es andere Anforderungen an Algorithmen. In Math.NET wird dies durch eine Gruppe von Generatorfunktionen abgebildet, die sich wie in Bild 5 gezeigt präsentieren.

Man wähle die gewünschte Zufallsart (Bild 5)
https://numerics.mathdotnet.com/RandomEin standardisiertes Interface ermöglicht dann, nach folgendem Schema Horden von Zufallszahlen zu beschaffen:
double[] samples = SystemRandomSource.Doubles(1000);
Alternativ dazu gibt es auch einen „Zufallszahlen-Iterator“, der nach dem folgenden Schema eine Sequenz von Zufallszahlen generieren kann:
System.Random random = new SystemRandomSource(); var sample = random.NextDouble();
Und jetzt mit symbolischer Mathematik
Der wichtigste und übrigens zulassungsentscheidende Unterschied zwischen verschiedenen Arten von wissenschaftlichen Taschenrechnern ist, ob sie symbolische Mathematik beherrschen. Darunter versteht man, dass das System „direkt“ mit Variablen arbeitet; der Code verdrahtet also Variablen und nicht Zahlen zu mathematischen Ausdrücken.
Zur Illustration der Möglichkeiten wollen wir nun in das aus dem vorangegangenen Artikel bekannte Beispiel zurückkehren, das im ersten Schritt das NuGet-Paket MathNet.Symbolic aufnimmt.
Für die effiziente Nutzung der im Paket enthaltenen Logik ist es danach empfehlenswert, wie hier gezeigt eine Using-Deklaration und einen Alias für die SymbolicExpression anzulegen:
using MathNet.Symbolics; using Expr = MathNet.Symbolics.SymbolicExpression;
Der einfachste Schritt zur Nutzung des Programms ist die Deklaration von Expression-Variablen, die danach mehr oder weniger beliebig weiterverarbeitet werden dürfen:
var x = Expr.Variable("x");
var a = Expr.Variable("a");
var b = Expr.Variable("b");
Für unsere Experimente interessanter ist die Möglichkeit, die Symbolics-Funktion gegen als Strings vorliegende Ausdrücke auszuführen. Für einen ersten Versuch bietet sich folgendes Snippet an:
var result = Expr.Parse("(a*x + b)");
var symbols = new Dictionary<string, FloatingPoint>
{{ "a", 2.0 },
{ "b", 3.0 },
{ "x", 1.0 }};
var outval = result.Evaluate(symbols);
Neben dem eigentlichen Ausdruck – er wandert in die Parse-Methode – ist auch ein Feld erforderlich, das die im Rahmen der Berechnung zu verwendenden Variablenwerte beschreibt. Ergebnis ist jedenfalls die Ausgabe der korrekten Lösung.
Im nächsten Schritt wollen wir das Programm wie folgt adaptieren, um die lineare Funktion in ein für ScottPlot verarbeitbares Format zu bringen:
double[] outVal = new double[50];
for (int i = 0; i < 50; i++)
{
symbols["x"] = i;
outVal[i] = result.Evaluate(symbols).RealValue;
}
MauiPlot1.Plot.Add.Signal(outVal);
Als Ergebnis erhalten wir die in Bild 6 gezeigte Darstellung.
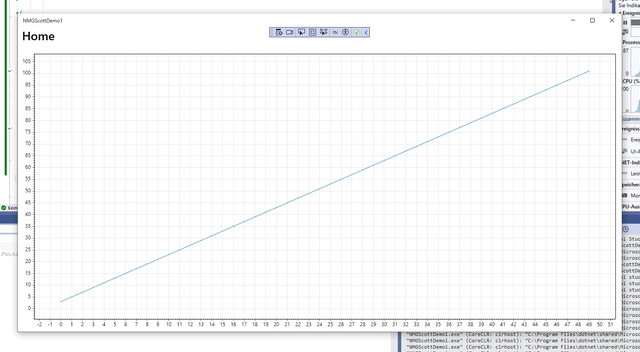
Math.NET hat seine Schuldigkeit getan (Bild 6)
AutorFazit
NuGet-Pakete stellen .NET-Entwicklern nicht nur GUI-Elemente, sondern auch Kernfunktionalität zur Verfügung. Das hier vorgestellte Math.NET bietet verschiedenste Hilfsfunktionen an – empfehlenswert für all jene, die sich mit Symbolik oder Simulation auseinandersetzen.