14. Sep 2020
Lesedauer 13 Min.
Bildinhalte erkennen und verarbeiten
OpenCV mit Python, Teil 1
Die freie Bibliothek OpenCV ermöglicht Bildverarbeitung und maschinelles Sehen. Sie wurde für die Programmiersprachen C/C++, Java und Python entwickelt.
dotnetpro
Die Stärken von OpenCV (Open Computer Vision) liegen in der Geschwindigkeit und der Modernität der eingebauten Algorithmen. In diesem Artikel und im nachfolgenden zweiten Teil wird ein Blick auf die Bibliothek OpenCV in der Version 4 geworfen.Diese Bibliothek ermöglicht einerseits die Bearbeitung von statischen und bewegten Bildern. In den entsprechenden Beispielen dieses Artikels geht es darum, ein Bild zu schärfen, die Farben zu manipulieren oder einen Ausschnitt festzulegen. Diese Methoden werden auch in der digitalen Fotografie in den diversen Bildbearbeitungsprogrammen angewendet.Andererseits geht es aber auch darum, zu erkennen, was auf den Bildern abgebildet ist, also ob dort ein Baum, ein Auto, eine Münze oder ein Gesicht zu sehen ist. Die erforderlichen Rechenalgorithmen sollen hier ebenfalls vorgestellt und an einfachen Szenarien angewendet werden.
Installation
In den folgenden Abschnitten wird die Programmiersprache Python benutzt, um die OpenCV-Bibliothek anzusprechen. Wenn Sie die Beispiele auf einem Windows-Rechner nachvollziehen wollen, sollten Sie mindestens Python 2.7 installiert haben [1]. Außerdem muss die Bibliothek numpy unbedingt vorhanden sein [2]. Schließlich können Sie OpenCV downloaden und durch einen Doppelklick installieren [3]. Nach der Installation kopieren Sie die Datei cv2.pyd aus dem Verzeichnis opencv\build\python\cv2\2.7\ in das Verzeichnis C:\Python27/lib/site-packages.Die erfolgreiche Installation kann anschließend geprüft werden. Im Kommandozeilenfenster von Windows rufen Sie Python auf und geben folgende import-Befehle ein:<span class="hljs-keyword">import</span> numpy
<span class="hljs-keyword">import</span> cv2
Wenn beide Befehle ohne Fehlermeldungen verarbeitet werden, ist der Rechner für die Bildverarbeitung mit OpenCV vorbereitet.Eine andere Möglichkeit ist die Benutzung der weit verbreiteten Anaconda-Installation zusammen mit Python 3. Hier können Sie OpenCV mit dem folgenden Befehl nachträglich installieren:
pip3 <span class="hljs-keyword">install</span> opencv-python
Die Installation unter Linux gestaltet sich in der Regel etwas komplizierter und soll nicht näher diskutiert werden. Hier ist es sehr sinnvoll, die Anaconda-Installation zu benutzen. Beachten Sie in diesem Fall die speziellen Build- und Installationshinweise für die unterschiedlichen Linux-Distributionen.
Erste Versuche
Wenn Sie sich die Demo-Dateien aus den Downloads zu diesem Artikel herunterladen, finden Sie dort auch ein Unterverzeichnis Images. Darin sind einige JPEG-Bilddateien abgelegt, die Sie für die ersten Experimente mit OpenCV benutzen können. Die Bilder habe ich entweder selbst fotografiert oder mit Grafikprogrammen erstellt; Sie können sie also nach Belieben einsetzen, ohne Urheberrechte zu verletzen.Im ersten Beispiel soll einfach eine JPEG-Bilddatei geladen und dargestellt werden:<span class="hljs-keyword">import</span> cv2
img = cv2.imread(‚.\<span class="hljs-type">Images</span>\<span class="hljs-type">Bild1_1024x683</span>.jpg‘)
cv2.imshow(‚<span class="hljs-type">Bild</span> 1‘, img)
cv2.waitKey(0)
Zunächst wird die Bibliothek OpenCV importiert. Die Funktion imread lädt dann eine JPEG-Datei. Das Bild wird im Objekt img abgelegt. Wenn man mit dem Befehl
<span class="hljs-keyword">type</span>(img)
den Typ des Bildobjekts abfragt, erhält man:
<<span class="hljs-keyword">type</span> <span class="hljs-type">‚numpy.ndarray‘> </span>
Die Bilddaten werden also in einem numpy-Array abgelegt. In der dritten Zeile des Beispiels wird das Bild für die Ausgabe in einem Fenster vorbereitet. In der letzten Zeile wird die Funktion waitKey aufgerufen, damit das Bild auch im Fenster dargestellt werden kann. Diese letzte Zeile müssen Sie auch eingeben, wenn Sie das Beispiel mit der Python-Konsole eingegeben haben.Mit dem Funktionsaufruf
<span class="hljs-selector-tag">cv2</span><span class="hljs-selector-class">.imwrite</span>(‚.\<span class="hljs-selector-tag">Images</span>\<span class="hljs-selector-tag">Bild1_neu</span><span class="hljs-selector-class">.jpg</span>‘. <span class="hljs-selector-tag">img</span>)
kann das Bildobjekt img in einer anderen Datei gespeichert werden. Dabei kann natürlich auch das Bildformat (zum Beispiel in PNG) geändert werden.Ein Farbbild kann auch in die einzelnen Farbkanäle (zum Beispiel: rot, grün und blau) zerlegt werden. In diesem Fall wird die split-Funktion angewendet, welche dann drei Arrays mit den jeweiligen Farbinformationen zurückliefert:
import cv<span class="hljs-number">2</span>
img = cv<span class="hljs-number">2.</span>imread<span class="hljs-comment">(‚.\Images\Bild1_1024x683.jpg‘)</span>
<span class="hljs-attr"># Kanäle aufspalten </span>
<span class="hljs-attr">g, b, r = cv2</span>.split<span class="hljs-comment">(img)</span>
<span class="hljs-attr"># Rot-Kanal darstellen </span>
<span class="hljs-attr">cv2</span>.imshow<span class="hljs-comment">("Rot", r)</span>
<span class="hljs-attr"># Kanäle zusammenfassen </span>
<span class="hljs-attr">img2</span> = cv<span class="hljs-number">2.</span>merge<span class="hljs-comment">((g, b, r)</span>)
cv<span class="hljs-number">2.</span>imshow<span class="hljs-comment">("RGB", img2)</span>
cv<span class="hljs-number">2.</span>waitKey<span class="hljs-comment">(0)</span>
Mit der merge-Funktion können einzelne Kanäle wieder zusammengefasst werden. Hierbei muss auf die richtige Schreibweise beim Funktionsaufruf geachtet werden: Der Parameter ist vom Typ tuple, darum müssen zwei runde Klammern benutzt werden: eine für den Funktionsaufruf, eine für die Tupel-Einfassung.Natürlich kann man die Kanäle mit der merge-Funktion auch in einer anderen Reihenfolge wieder zusammenführen, allerdings wird das Ergebnis dann farblich wohl etwas fragwürdig sein.Um auf einzelne Pixel der Bilder zuzugreifen, benutzt man einfach die Array-Schreibweise der numpy-Arrays (ndarray). Diese Arrays wurden in [4] ausführlich vorgestellt. Anknüpfend an das letztgenannte Beispiel kann man auf die Pixeldaten folgendermaßen zugreifen:
print(r[<span class="hljs-number">0</span>,<span class="hljs-number">0</span>]) # Pixel(<span class="hljs-number">0</span>,<span class="hljs-number">0</span>)
print(g[<span class="hljs-number">4</span>,<span class="hljs-number">7</span>]) # Pixel(<span class="hljs-number">4</span>,<span class="hljs-number">7</span>)
# Das Farb-Image besteht aus drei Kanälen
# <span class="hljs-number">3.</span> Index ist der Farbkanal
print(img[<span class="hljs-number">0</span>,<span class="hljs-number">0</span>,<span class="hljs-number">0</span>]) # Pixel(<span class="hljs-number">0</span>,<span class="hljs-number">0</span>) Kanal grün
print(img[<span class="hljs-number">3</span>,<span class="hljs-number">5</span>,<span class="hljs-number">2</span>]) # Pixel(<span class="hljs-number">3</span>,<span class="hljs-number">5</span>) Kanal rot
Die drei Images r,g und b bestehen nur aus jeweils einem Kanal. Hier werden nur zwei Indizes (x- und y-Koordinate) für die Adressierung benötigt. Wenn auf das Farbbild img zugegriffen wird, müssen drei Indizes angegeben werden: die x- und die y-Koordinate sowie der gewünschte Farbkanal.Natürlich gibt es in der OpenCV-Bibliothek auch Funktionen, um die Helligkeit oder den Kontrast eines Schwarz-Weiß- oder Farbbildes anzupassen.
Transformationen
Mit OpenCV kann man jedoch auch wesentlich interessantere Aufgaben erledigen. Zum Beispiel lassen sich affine Transformationen durchführen. Dazu gehören Verschiebungen (Translation), Drehungen (Rotation) oder Größenänderungen (Skalierung). Bei affinen Transformationen bleiben gerade Linien erhalten, aus Quadraten können aber Rechtecke oder Parallelogramme werden. Es können sich also die Längen und Winkel ändern.Solche Transformationen sind mathematisch gesehen nichts weiter als einfache Matrixmultiplikationen. Für eine kleine Auffrischung der mathematischen Kenntnisse helfen zum Beispiel [5] oder [6].Im zweidimensionalen Raum sind die Transformationsmatrizen 2 x 2 (Drehung) oder 2 x 3 (Skalierung und Verschiebung) Elemente groß. Eine solche Verschiebungsmatrix sieht dann folgendermaßen aus: |<span class="hljs-string"> 1 0 tx </span>|<span class="hljs-string"> </span>
<span class="hljs-string">T = </span>|<span class="hljs-string"> </span>|<span class="hljs-string"> </span>
<span class="hljs-string"> </span>|<span class="hljs-string"> 0 1 ty </span>|<span class="hljs-string"> </span>
Die beiden Platzhalter tx und ty stehen für die Verschiebung in der x- und y-Richtung. Mit dieser Matrix wird das Bild nicht vergrößert oder verkleinert, da die beiden Skalierungsfaktoren auf 1 gesetzt wurden. In Listing 1 wird an diesen Stellen der Wert 0,5 verwendet, da das Bild in beiden Koordinatenachsen auf die Hälfte verkleinert werden soll.
Listing 1: Affine Transformationen
<span class="hljs-keyword">import</span> cv2 <br/><span class="hljs-keyword">import</span> numpy <span class="hljs-keyword">as</span> np <br/><br/># Bild einlesen <br/>img = cv2.imread(<span class="hljs-string">".\Images\Bild1_1024x683.jpg"</span>) <br/>rows, cols = img.shape[:<span class="hljs-number">2</span>] <br/><br/># Halbe Größe und <span class="hljs-keyword">in</span> die Mitte verschieben <br/>trans_mat = np.float32([[<span class="hljs-number">0.5</span>, <span class="hljs-number">0</span>, cols / <span class="hljs-number">4</span>], <br/> [<span class="hljs-number">0</span>, <span class="hljs-number">0.5</span>, rows / <span class="hljs-number">4</span>]]) <br/>img2 = cv2.warpAffine(img, trans_mat, (cols, rows), <br/> cv2.INTER_LINEAR) <br/>rows2, cols2 = img2.shape[:<span class="hljs-number">2</span>] <br/><br/># Drehung um <span class="hljs-number">25</span>° im Uhrzeigersinn <br/>rot_mat = cv2.getRotationMatrix2D((cols2 / <span class="hljs-number">2</span>, <br/> rows2 / <span class="hljs-number">2</span>), <span class="hljs-number">-25</span>, <span class="hljs-number">1</span>) <br/>img3 = cv2.warpAffine(img2, rot_mat, (cols2, rows2)) <br/><br/># Fenster anlegen und Größe festlegen <br/>cv2.resizeWindow(<span class="hljs-string">""</span>, cols, rows) <br/>cv2.imshow(<span class="hljs-string">"Translation+Rotation"</span>, img3) <br/><br/># Warten, dann alle Fenster schließen <br/>cv2.waitKey(<span class="hljs-number">0</span>); <br/>cv2.destroyAllWindows()
In einer Drehmatrix befinden sich verschiedene Sinus- und Cosinuswerte vom jeweils gewünschten Drehwinkel:
|<span class="hljs-string"> cos 0 -sin 0 </span>|<span class="hljs-string"> </span>
<span class="hljs-string">T = </span>|<span class="hljs-string"> </span>|<span class="hljs-string"> </span>
<span class="hljs-string"> </span>|<span class="hljs-string"> sin 0 cos 0 </span>|<span class="hljs-string"> </span>
Wenn nun ein Pixel des Bildes an eine andere Stelle transformiert werden soll, dann muss man die Koordinaten des Pixels (x1, y1) mit der Transformationsmatrix multiplizieren. Dabei erhält man die neuen Koordinaten des Pixels (x2, y2).Gehen wir das Programm aus Listing 1 nun Schritt für Schritt durch. Nach dem Import der benötigten Bibliotheksmodule wird zunächst ein Farbbild mit imread eingelesen. Danach werden Zeilen- und Spaltenanzahl des Bildes ermittelt. Mit der shape-Funktion werden die Größe des Bildes (Zeilen und Spalten) und die Anzahl der Farbkanäle in ein Tupel zurückgegeben. Da wir hier im Beispiel nur die Zeilen- und Spaltenanzahl benötigen, verwenden wir nur die ersten beiden Zahlen aus dem Ergebnis-Tupel.Listing 1 führt gleich mehrere Transformationen aus. Zunächst wird das geladene Bild img auf die halbe Größe verkleinert und dann in die Mitte des Fensters geschoben. Das Ergebnis wird in der Variablen img2 abgelegt. Im zweiten Schritt wird das Bild img2 um 25 Grad im Uhrzeigersinn gedreht. Das Endergebnis wird im Objekt img3 gespeichert und in einem Fenster ausgegeben.Beide Transformationen werden mit der OpenCV-Funktion warpAffine ausgeführt. Vorher werden die jeweils benötigten Transformationsmatrizen mit np.float32 angelegt. Hierbei handelt es sich um Fließkomma-Arrays aus der numpy-Bibliothek. Der Skalierungsfaktor ist 0,5, und das Bild wird um ein Viertel der Bildhöhe (rows) nach unten sowie um ein Viertel der Bildbreite (cols) nach rechts verschoben. Dadurch steht das verkleinerte Bild wieder genau in der Mitte des Fensters. Beim Aufruf von warpAffine werden einfach nur das Image-Objekt, die angelegte Transformationsmatrix und die Bildgröße als Tupel übergeben.Danach wird die neue Bildgröße ermittelt und in den Variablen rows2 und cols2 abgelegt. Die neue Bildgröße muss bei der zweiten Transformation (Drehung) berücksichtigt werden. Zunächst wird mit der OpenCV-Funktion getRotationMatrix2D die erforderliche Transformationsmatrix erstellt. Der erste Parameter der Funktion ist ein Tupel und enthält den gewünschten Drehpunkt im Bild. In unserem Fall ist das genau die Bildmitte (cols2 / 2 und rows2 / 2). Danach wird der Drehwinkel in Altgrad angegeben. Eine positive Zahl lässt den Winkel gegen den Uhrzeigersinn laufen, eine negative Zahl gibt einen Winkel im Uhrzeigersinn an. OpenCV berechnet die benötigten Sinus- und Cosinuswerte und setzt sie an den richtigen Stellen in die Transformationsmatrix ein.Der dritte Parameter erlaubt wieder die Eingabe eines Skalierungswerts. Dieser ist in unserem Beispiel jedoch auf den Wert 1 gesetzt.Nun kann die Funktion warpAffine mit den bekannten Parametern aufgerufen werden.Abschließend erstellt die Funktion resizeWindow ein Fenster in der ursprünglichen Bildgröße. Das transformierte Bild wird mit imshow ausgegeben. Nach dem Schließen des Ausgabefensters zerstört die Funktion destroyAllWindows alle offenen Fenster. Das Ergebnis ist in Bild 1 gezeigt.
Transformationenmit OpenCV(Bild 1)
Autor
Ganz allgemein kann man affine Transformationen auch durch drei Punktepaare darstellen. Dabei werden drei Punkte im Quellbild auf drei Punktepaare im Zielbild abgebildet.Als Beispiel können wir folgende affine Transformation ausführen: Der erste Punkt (links oben) des Quellbilds soll im Zielbild an der gleichen Stelle bleiben (Bild 2). Der zweite Punkt (rechts oben) soll im Zielbild etwa oben in der Mitte liegen. Der dritte Punkt des Quellbilds (links unten) soll im Zielbild ungefähr unten in der Mitte liegen. Alle Bildpunkte werden nun in diese Transformation hineingerechnet. Dazu muss mit der OpenCV-Funktion getAffineTransform von den beiden 3-Punkte-Arrays die Transformationsmatrix erstellt und angewendet werden. Den erforderlichen Code zeigt Listing 2.
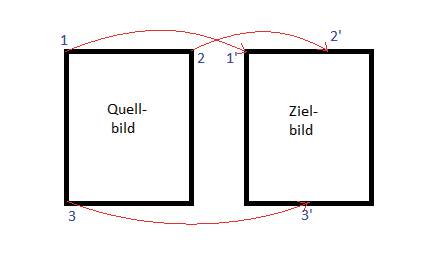
Affine Transformationmit drei Punkten(Bild 2)
Autor
Listing 2: Ein schräg verzerrtes Bild
import cv2 <br/>import numpy as np <br/><br/># Bild einlesen <br/>img = cv2.imread(<span class="hljs-string">".\Images\Bild1_1024x683.jpg"</span>) <br/>rows, cols = img.shape[:<span class="hljs-number">2</span>] <br/><br/># Drei-Punkte-Arrays für Quell- und Zielbild <br/>quell_punkte = np.float32(<span class="hljs-string">[[0, 0], [cols - 1, 0], </span><br/><span class="hljs-string"> [0, rows - 1]]</span>) <br/>ziel_punkte = np.float32(<span class="hljs-string">[[0, 0], [int(cols / 2), </span><br/><span class="hljs-string"> 0], [int(cols / 2), rows - 1]]</span>) <br/><br/># Transformationsmatrix erzeugen und Bild <br/># transformieren <br/>matrix = cv2.getAffineTransform(quell_punkte, <br/> ziel_punkte) <br/>img_neu = cv2.warpAffine(img, matrix, (cols, rows)) <br/><br/># Bilder ausgeben <br/>cv2.imshow(<span class="hljs-string">"Original"</span>, img) <br/>cv2.imshow(<span class="hljs-string">"Transformiert"</span>, img_neu) <br/>cv2.waitKey(<span class="hljs-number">0</span>)
Nach dem Einlesen des Bildes in die Variable img werden die Arrays für die Punkte im Quell- und im Zielbild erzeugt (quell_punkte und ziel_punkte). Die Punkte werden wiederum als kleine Arrays für die Spalten- und Zeilenposition angegeben, wie in Tabelle 1 zu sehen.
Tabelle 1: Punkte-Arrays für Quell- und Zielbild
|
Nachdem die Punkte-Arrays erstellt wurden, kann in der nächsten Programmzeile die Transformationsmatrix mit getAffineTransform aufgebaut werden. Schließlich wird die Transformation wieder mit der bereits bekannten Funktion warpAffine ausgeführt und die Bilder mit imshow in Fenstern dargestellt. Das Ergebnis zeigt Bild 3: Das Bild hat nun die Form eines Parallelogramms.
Das schräg verzerrte Bildnach der Transformation(Bild 3)
Autor
Ein weiteres wichtiges Feature der OpenCV-Bibliothek sind die projektiven Transformationen. Diese werden sehr häufig benötigt, da ein zweidimensionales Bild immer eine Projektion ist. Wenn man ein Quadrat senkrecht von oben fotografiert, erhält man in der Bilddarstellung auch wieder ein Quadrat. Fotografiert man jedoch von schräg oben, so erhält man ein Rechteck, das im oberen Bildteil immer schmaler wird (Bild 4).
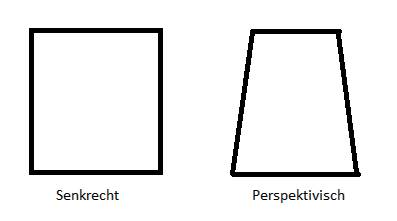
Perspektivische Darstellungvon Bildinhalten(Bild 4)
Autor
Um die Inhalte solcher Fotos besser analysieren zu können, lässt sich die Perspektive im Bild durch eine Transformation wegrechnen. Auch hierbei werden zwei Arrays mit den Punkten im Quellbild und im Zielbild assoziiert. Mit der OpenCV-Funktion getPerspectiveTransform wird die erforderliche Transformationsmatrix erstellt und mit der Funktion warpPerspective auf das Quellbild angewendet:
<span class="hljs-meta"># Perspektivische Transformation </span>
<span class="hljs-meta">cv2.getPerspectiveTransform(quell_punkte, ziel_punkte) </span>
<span class="hljs-meta">img_neu = cv2.warpPerspective(img, matrix, (cols, rows)) </span>
Es gibt noch weitere interessante Transformations-Varianten in OpenCV, die hier aber nicht weiter besprochen werden, da sie den Rahmen des Artikels sprengen würden.
Faltungen
Nein, es soll jetzt kein Kapitel über Origami folgen. Faltungen sind grundlegende Operationen in der Bildbearbeitung. Diese Operationen verändern die Pixel im Bild in irgendeiner Weise. Man spricht in diesem Zusammenhang auch von Filter-Operationen. Auf der einen Seite hat man das Bild als Pixel-Matrix, auf der anderen Seite gibt es einen Kernel, der mit dem Bild verknüpft wird. Dieser Kernel ist auch wieder eine (meistens sehr kleine) Matrix, die irgendwelche Zahlen enthält.Die einfachste Kernel-Matrix, die man sich vorstellen kann, ist die Identitätsmatrix I: | <span class="hljs-number">0</span> <span class="hljs-number">0</span> <span class="hljs-number">0</span> |
I = | <span class="hljs-number">0</span> <span class="hljs-number">1</span> <span class="hljs-number">0</span> |
| <span class="hljs-number">0</span> <span class="hljs-number">0</span> <span class="hljs-number">0</span> |
Wenn ein Bild mit dieser Matrix multipliziert wird, dann ist das Ergebnis wieder genau das gleiche Bild.In Bild 5 wird die Vorgehensweise gezeigt. Das Pixel-Bild ist hier der gesamte Kasten mit allen weißen Kästchen. Das Pixel des Bildes, das gerade rechnerisch bearbeitet wird, ist das tiefschwarze Kästchen. Der Kernel (hier die Identitätsmatrix) wird durch die neun hellgrauen Kästchen repräsentiert. Die entsprechenden Matrixwerte sind hier eingetragen.
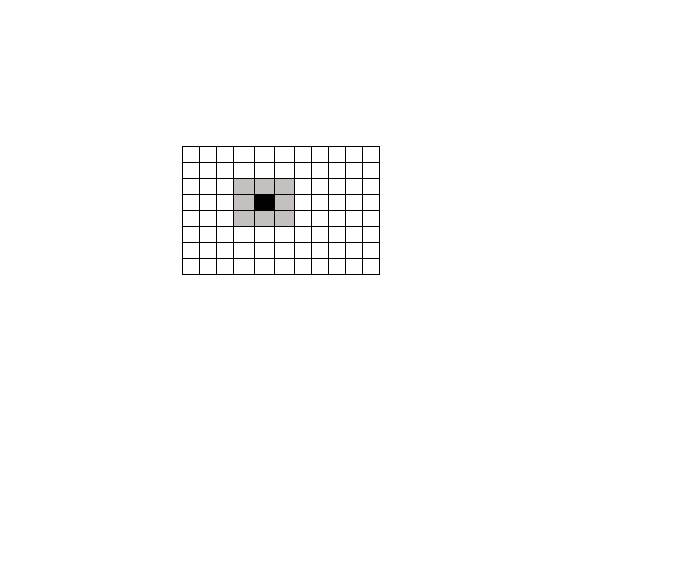
Eine Faltungmit I(Bild 5)
Autor
Nun werden die neun Werte im Bild-Array mit den neun Werten, die im Kernel-Array stehen, multipliziert und summiert. Das Ergebnis wird in ein zweites Bild-Array an die Position des schwarzen Kästchens geschrieben. Auf diese Weise entsteht dann Schritt für Schritt das neue, „gefilterte“ Bild.Wie man leicht erkennen kann, verändert die Identitätsmatrix das Bild tatsächlich nicht, denn nur das zentrale Pixel geht in das neue Bild ein. Alle anderen Pixel werden mit null multipliziert und werden gar nicht berücksichtigt. Hier kann man schon erkennen, dass bei großen Bildern und großen Kerneln sehr viele mathematische Operationen (Additionen und Multiplikationen) ausgeführt werden müssen.Ein weiterer sehr einfacher Filter ist der Low-Pass-Filter. Er mittelt mithilfe eines Kernels L die Werte mehrerer Pixel. Dabei entsteht ein unscharfes Bild.
| <span class="hljs-number">1</span> <span class="hljs-number">1</span> <span class="hljs-number">1</span> |
L = (<span class="hljs-number">1</span>/<span class="hljs-number">9</span>) * | <span class="hljs-number">1</span> <span class="hljs-number">1</span> <span class="hljs-number">1</span> |
| <span class="hljs-number">1</span> <span class="hljs-number">1</span> <span class="hljs-number">1</span> |
Da in diesem Fall die Werte von neun Pixeln addiert werden, muss das Ergebnis noch durch neun dividiert werden, damit das entstehende Bild nicht heller ist als das Ausgangsbild.Listing 3 zeigt die Verwendung unterschiedlicher Unschärfe-Filter mit OpenCV.
Listing 3: Filter anwenden
<span class="hljs-keyword">import</span> cv2 <br/><span class="hljs-keyword">import</span> numpy <span class="hljs-keyword">as</span> np <br/><br/># Eingabe der Kernel-Größe <br/>strInput = input(<span class="hljs-string">"Kernel-Größe eingeben (3, 5, 7, </span><br/><span class="hljs-string"> 9,...): "</span>) <br/>iSize = int(strInput) <br/><br/># Bild einlesen <br/>img = cv2.imread(<span class="hljs-string">".\Images\Bild1_1024x683.jpg"</span>) <br/><br/># Kernel <span class="hljs-keyword">in</span> der Größe (iSize x iSize) erzeugen und <br/># normieren <br/>kernel = np.ones((iSize, iSize), np.float32) / <br/> (iSize * iSize) <br/><br/># Filter anwenden <br/>img_neu = cv2.filter2D(img, <span class="hljs-number">-1</span>, kernel) <br/><br/># Ergebnisbild ausgeben <br/>cv2.imshow(<span class="hljs-string">"Unscharf"</span>, img_neu) <br/>cv2.waitKey(<span class="hljs-number">0</span>)
Mit dem Beispielprogramm in Listing 3 können Sie verschiedene Kernel-Größen auf das Ausgangsbild anwenden. Je größer der Kernel gewählt wird, desto mehr Pixelwerte werden gemittelt und desto unschärfer wird das Ergebnisbild.Der Kernel kann in diesem Fall einfach mit der Funktion np.ones(…) aus der numpy-Bibliothek erzeugt werden. Es wird zunächst die gewünschte Größe des Einer-Arrays angegeben und danach der erforderliche Typ (hier: Fließkomma). Die eigentliche Rechenoperation wird in der OpenCV-Funktion filter2D ausgeführt. Der erste Parameter ist das Image, auf das der Filter angewendet werden soll, und der dritte Parameter ist die Kernel-Matrix. Der zweite Parameter gibt an, mit welchem Datentyp das Ergebnisbild erstellt werden soll. Wenn dort -1 angegeben wird, wird der Typ des Ausgangsbildes benutzt.Je nachdem, mit welchen Zahlenwerten die Kernel-Matrix belegt ist, werden unterschiedliche Ergebnisse erzielt. Ein Kernel, der ein Bild schärfen soll, kann folgendermaßen aussehen:
| <span class="hljs-number">-1</span> <span class="hljs-number">-1</span> <span class="hljs-number">-1</span> |
M = | <span class="hljs-number">-1</span> <span class="hljs-number">9</span> <span class="hljs-number">-1</span> |
| <span class="hljs-number">-1</span> <span class="hljs-number">-1</span> <span class="hljs-number">-1</span> |
Es kann wieder der Code aus Listing 3 benutzt werden. Sie müssen nur die neue Kernel-Matrix erstellen und den Eingabe-Code entfernen:
kernel = np.array([[<span class="hljs-number">-1</span>, <span class="hljs-number">-1</span>, <span class="hljs-number">-1</span>],
[<span class="hljs-number">-1</span>, <span class="hljs-number">9</span>, <span class="hljs-number">-1</span>], [<span class="hljs-number">-1</span>, <span class="hljs-number">-1</span>, <span class="hljs-number">-1</span>]]) Ermittlung von Kanten
Ein weiteres wichtiges Verfahren bei der Bildverarbeitung ist die Kantenermittlung (auf Englisch: edge detecting). Wie kann man die Kanten eines Objekts ermitteln? Eigentlich ist es (zunächst) ganz einfach. Bei einem Schwarz-Weiß-Bild ist eine Kante dort, wo Hell in Dunkel übergeht, oder umgekehrt. Wenn man also ein Schwarz-Weiß-Bild Pixel für Pixel auf solche großen Helligkeitunterschiede untersucht, dann sollte man alle Kanten finden. Leider ist es nicht ganz so einfach. Man kann zum Beispiel die Pixel horizontal oder vertikal abarbeiten. Außerdem liegen in der Regel Farbbilder vor, sodass man drei Kanäle analysieren muss.Für mathematisch interessierte Leser lässt sich das Problem folgendermaßen beschreiben: Kanten sind dann gegeben, wenn der Betrag des Gradienten (die erste Ableitung in x- und y-Richtung) der Helligkeit im Bild an der Position (x, y) groß ist.Zum Glück haben wir die OpenCV-Bibliothek. Dort findet man mehrere Algorithmen, mit denen Kanten ermittelt werden können. Das einfachste Verfahren wird durch den Sobel-Algorithmus implementiert. Hierbei wird eine Faltung (siehe das vorangegangene Beispiel) mit folgenden Matrizen ausgeführt: | <span class="hljs-number">-1</span> <span class="hljs-number">0</span> <span class="hljs-number">1</span> |
Sh = | <span class="hljs-number">-2</span> <span class="hljs-number">0</span> <span class="hljs-number">2</span> |
| <span class="hljs-number">-1</span> <span class="hljs-number">0</span> <span class="hljs-number">1</span> |
| <span class="hljs-number">-1</span> <span class="hljs-number">-2</span> <span class="hljs-number">-1</span> |
Sv = | <span class="hljs-number">0</span> <span class="hljs-number">0</span> <span class="hljs-number">0</span> |
| <span class="hljs-number">1</span> <span class="hljs-number">2</span> <span class="hljs-number">1</span> |
Die erstgenanne Matrix Sh liefert mit dem Aufruf der OpenCV-Funktion Sobel die horizontalen, die zweite Matrix Sv die vertikalen Kanten.Listing 4 zeigt die Anwendung des Sobel-Filters. Um die Sache etwas übersichtlicher zu gestalten, befindet sich in den Downloads zum Artikel in dem Verzeichnis .\Images die Datei Bild2.jpg. Diese Datei enthält ein Bild, das nur aus senkrechten, waagerechten und schrägen Linien besteht. Im Anschluss an das Einlesen der Datei als Schwarz-Weiß-Bild kann sofort die Sobel-Funktion angewendet werden. Als Parameter werden das Bild-Objekt, das Zielformat des Bildes, die Ordnungen der Ableitung in x- und y-Richtung sowie die Kernel-Größe (hier: 5) angegeben.
Listing 4: Kantenermittlung – Version 1
import cv2 <br/>import numpy as np <br/><br/># Bild einlesen <br/>img = cv2.imread(<span class="hljs-string">".\Images\Bild2.jpg"</span>, <br/> cv2.IMREAD_GRAYSCALE) <br/><br/># Sobel-Filter horizontal / vertikal <br/>img_vert = cv2.Sobel(img, cv2.CV_8U, <span class="hljs-number">1</span>, <span class="hljs-number">0</span>, <br/> ksize = <span class="hljs-number">5</span>) <br/>img_horz = cv2.Sobel(img, cv2.CV_8U, <span class="hljs-number">0</span>, <span class="hljs-number">1</span>, <br/> ksize = <span class="hljs-number">5</span>) <br/><br/># Ergebnisbilder ausgeben <br/>cv2.imshow(<span class="hljs-string">"Das Bild"</span>, img) <br/>cv2.imshow(<span class="hljs-string">"Kanten horz."</span>, img_horz) <br/>cv2.imshow(<span class="hljs-string">"Kanten vert."</span>, img_vert) <br/>cv2.waitKey(<span class="hljs-number">0</span>)
Beim ersten Filter wird die Ableitung erster Ordnung in x-Richtung benutzt. Im Ergebnisbild img_vert können Sie alle vertikalen und schrägen Kanten erkennen. Die genau horizontalen Kanten sind in diesem Bild nicht zu erkennen (Bild 6). Im Bild img-horz werden dagegen alle horizontalen und schrägen Kanten dargestellt.
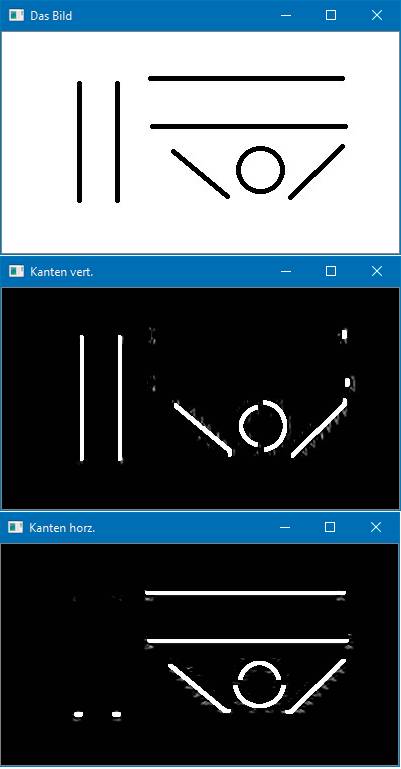
Kantenmit dem Sobel-Algorithmus(Bild 6)
Autor
Wenn Sie sowohl horizontale als auch vertikale Kanten im Ergebnisbild erhalten wollen, können Sie die Funktion Laplacian verwenden:
<span class="hljs-attr">img_kanten</span> = cv2.Laplacian(img, cv2.CV_8U)
Die Laplacian-Funktion liefert das gewünschte Ergebnis, nämlich alle Kanten. Wenn diese Funktion allerdings auf ein normales Foto angewendet wird, ist das erzeugte Kanten-Bild meistens sehr verrauscht, das heißt, die Kanten sind nur sehr schlecht zu erkennen.Hier hilft die Canny-Funktion weiter:
<span class="hljs-attr">img_kanten</span> = cv2.Canny(img, <span class="hljs-number">100</span>, <span class="hljs-number">240</span>)
Das vollständige Beispiel finden Sie als Listing 5 in den Downloads zum Artikel. Die Canny-Funktion wird mit dem Eingabe-Bild und einem unteren (hier: 100) und einem oberen Grenzwert (hier: 240) aufgerufen. Das erstellte Kanten-Bild (Bild 7) ist qualitativ gut recht gut interpretierbar. Die Wahl der beiden Grenzwerte ist für die Qualität des Ergebnisbilds sehr wichtig. Mit ihnen lässt sich sehr genau angeben, wie stark die Kanten ausgeprägt sein müssen (also die Helligkeitsdifferenz), damit sie im Ergebnisbild erscheinen.
Kantenmit dem Canny-Algorithmus(Bild 7)
Autor
Die unterschiedlichen Kantenalgorithmen sind für die Erkennung von Objekten entscheidend. Im genannten Verzeichnis .\Images finden Sie das Foto Bild3.jpg, das nur Schrauben und Muttern zeigt. Wenn wir die Objekte im Bild zählen wollen, können wir das Bild mit dem Canny-Algorithmus auf die jeweiligen Umrisse der Objekte beschränken und so die weitere Auswertung stark vereinfachen. Bild 8 zeigt die Anwendung auf die Datei Bild3.jpg (das vollständige Beispiel finden Sie in den Downloads zum Artikel als Listing 6).
Der Canny-Algorithmusmit Schrauben und Muttern(Bild 8)
Autor
Man erkennt aber auch hier noch Probleme. Nicht gewollte Helligkeitsunterschiede (Reflexionen, Schatten …) machen bei der Auswertung Schwierigkeiten und müssen entweder vermieden oder weggerechnet werden.
Erweiterungs- und Erosionsfilter
Die letzten beiden Filter, die in diesem Artikel angesprochen werden sollen, sind Erweiterungs- und Erosionsfilter. Der Erweiterungsfilter (auf Englisch: dilation) erweitert oder verstärkt ein Bildobjekt, einfach ausgedrückt: Die Objekte werden „dicker“. Der Erosionsfilter macht die Objekte entsprechend „dünner“. Die beiden Filter kann man sehr schnell mit mit dem Code aus Listing 7 ausprobieren.Listing 7: Erweiterungs- und Erosionsfilter
<span class="hljs-keyword">import</span> cv2 <br/><span class="hljs-keyword">import</span> numpy <span class="hljs-keyword">as</span> np <br/><br/># Einfaches Test-Bild einlesen <br/>img = cv2.imread(<span class="hljs-string">".\Images\Bild2.jpg"</span>, <br/> cv2.IMREAD_GRAYSCALE) <br/><br/># Kernel aus Eins-Werten erzeugen <br/>kernel = np.ones((<span class="hljs-number">5</span>, <span class="hljs-number">5</span>), np.uint8) <br/><br/># Erosion und Erweiterung <br/>img_eros = cv2.erode(img, kernel, iterations = <span class="hljs-number">1</span>) <br/>img_dila = cv2.dilate(img, kernel, iterations = <span class="hljs-number">1</span>) <br/><br/># Bilder ausgeben <br/>cv2.imshow(<span class="hljs-string">"Input-Bild"</span>, img) <br/>cv2.imshow(<span class="hljs-string">"Erosion"</span>, img_eros) <br/>cv2.imshow(<span class="hljs-string">"Dilation"</span>, img_dila) <br/>cv2.waitKey(<span class="hljs-number">0</span>)
Für die beiden Filter wird ein Kernel aus Eins-Werten erstellt. Mit den OpenCV-Funktionen erode und dilate können die neuen Bilder erzeugt werden. In den Funktionsaufrufen werden das Ausgangsbild, die Kernel-Matrix und die Anzahl der Kernel-Anwendungen angegeben. Je öfter der Kernel angewendet wird, desto stärker ist der jeweilige Effekt. Bedenken Sie dabei jedoch, dass bei mehrfacher Anwendung des Erosionsfilters einzelne Objekte des Bildes komplett verschwinden können. Bild 9 zeigt die Ergebnisse mit dem Beispielprogramm aus Listing 7.
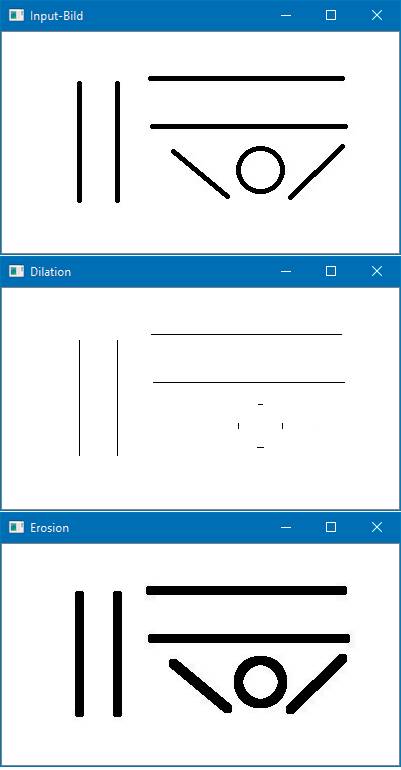
Der Erosions- und der Erweiterungsfilterim Einsatz(Bild 9)
Autor
Zusammenfassung
Der erste Artikel über OpenCV hat zunächst die grundlegenden und wichtigen Bildbearbeitungsalgorithmen vorgestellt, die angewendet werden müssen, bevor ein Bild (oder eine Bildfolge) analysiert werden kann.Im zweiten Artikel werden Sie die Analysealgorithmen von OpenCV kennenlernen. Wie können Strukturen in einem Bild ermittelt werden? Wie kann man ein Gesicht erkennen? Diese und andere Fragen werden im nächsten Artikel angesprochen. Es werden die erforderlichen OpenCV-Funktionen vorgestellt und mit Python-Programmen ausprobiert.Fussnoten
- Python-Download, http://www.dotnetpro.de/SL2010OpenCV1
- numpy-Download, http://www.dotnetpro.de/SL2010OpenCV2
- OpenCV-Download, https://opencv.org/releases/
- Bernd Marquardt, Arrays mit Schleife, Mathematik mit Python, Teil 1, dotnetpro 12/2017, Seite 64 ff., http://www.dotnetpro.de/A1712Rechnen
- Grundlagen der Matrizenmultiplikation, http://www.dotnetpro.de/SL2010OpenCV3
- Schreibweisen der Matrizenmultiplikation, http://www.dotnetpro.de/SL2010OpenCV4
