11. Dez 2023
Lesedauer 14 Min.
Lösungen entwickeln mit Excel
Algorithmen für maschinelles Lernen
Excel als Basis für die Entwicklung von Algorithmen für Machine Learning nutzen.

Maschinelles Lernen und Deep Learning sind inzwischen zu wichtigen Bestandteilen in vielen Anwendungen geworden, die täglich in den unterschiedlichsten Bereichen genutzt werden.Excel ist ein ausgezeichnetes Tool für die Datenanalyse von kleinen bis mittleren Datenmengen. Für viele Fälle bietet die Tabellenkalkulation alles, was der Anwender benötigt: Ansichten, Diagramme, komplexe Rechenfunktionen sowie die Möglichkeit, Makros zu erstellen oder VBA-Code zu schreiben. Excel will und kann allerdings in keiner Weise die Implementierung von maschinellem Lernen in einer Programmiersprache wie zum Beispiel Python ersetzen. Aber es ist ein großartiges Programm, um die Grundlagen der KI zu erlernen und grundlegende Probleme zu lösen, ohne eine Zeile Code schreiben zu müssen.Das liegt daran, dass Excel nicht nur eine einfache Tabellenkalkulation ist, in der Daten in Tabellenform gespeichert werden, sondern ein sehr leistungsfähiges Tool mit zahlreichen Funktionen, die es ermöglichen, Modelle des Machine Learning direkt auf dem Arbeitsblatt (Worksheet) zu erstellen. Excel kann diese Daten in kürzester Zeit analysieren und konsistente Ergebnisse liefern.Eine wichtige Lösung im Bereich Machine Learning ist zum Beispiel die lineare Regression, die zur Analyse von Daten und zur Vorhersage von Ergebnissen verwendet wird. Mit Excel ist es möglich, Regressionsmodelle aus tabellarischen Dateneingaben in der Tabellenkalkulation zu erstellen.Grundlegende Excel-Formeln wie SUMME und SUMMENPRODUKT können Sie beim schrittweisen Aufbau einer linearen Regression unterstützen. Neben der Regression lassen sich über Formeln und Funktionen wie INDEX, ADRESSE, MITTELWERTWENN (AVERAGEIF) und WENN beispielsweise Daten aus Clusterzentren berechnen und verfeinern. Somit ist es mit Excel möglich, Cluster zu verfolgen und zu überwachen.Des Weiteren ist es in Excel möglich, über das Datendiagramm-Objekt ein Modell für Machine Learning zu erstellen, um Änderungen in Datenwerten vorherzusagen.Das Diagramm-Objekt verfügt außerdem über eine Funktion mit der Bezeichnung Trendlinie, mit der aus Daten ein Regressionsmodell erstellt werden kann. Die Trendlinie kann auf verschiedene Arten von Regressionsalgorithmen eingestellt werden. Das Diagramm-Objekt kann so konfiguriert werden, dass es die Parameter des Machine-Learning-Modells anzeigt. Einem einzigen Diagramm können auch mehrere Trendlinien hinzugefügt werden, was den Prozess des Testens und Vergleichens der Leistungen verschiedener ML-Modelle anhand derselben Daten ermöglicht.Dieser Artikel will zeigen, wie Sie als Lernprojekt für Ausbildung, Studium oder Hobby einen Machine-Learning-Algorithmus in Excel ohne Programmiercode erstellen. Das Ziel ist die Implementierung des k-nächste-Nachbarn-Algorithmus (k-Nearest-Neighbor) als Klassifizierungsmodell für den Trainingsdatensatz der Iris-Blüten (Iris Flower) [1].
einen Input auf eine Klasse abbildet.Das heißt, der unbekannte Input soll einer Klasse, welche die Kategorie darstellt, zugeordnet werden.Somit besteht das Ziel darin, passende Regeln zu finden, nach denen sich die Daten der jeweiligen Klasse zuordnen lassen. Bei einer Klassifizierung steht schon im Vorfeld fest, in welche Gruppe ein Objekt eingeordnet werden kann.Hier geht es hauptsächlich darum, die Merkmale zu identifizieren, die für die Zuordnung am erkennbarsten sind. Beispiele für die bekanntesten Klassifizierungsaufgaben sind:
Klassifizierung
Das nachfolgende Beispiel zeigt die Erstellung eines Machine-Learning-Modells für die Klassifikation. Das Klassifikationsverfahren teilt Objekte nach ihren Merkmalen anhand eines Klassifizierungsmodells (Klassifikator) in vordefinierte Kategorien ein.Das Machine-Learning-Modell (ML-Modell), in diesem Fall der Klassifikator, ist eine mathematische Funktion, dieeinen Input auf eine Klasse abbildet.Das heißt, der unbekannte Input soll einer Klasse, welche die Kategorie darstellt, zugeordnet werden.Somit besteht das Ziel darin, passende Regeln zu finden, nach denen sich die Daten der jeweiligen Klasse zuordnen lassen. Bei einer Klassifizierung steht schon im Vorfeld fest, in welche Gruppe ein Objekt eingeordnet werden kann.Hier geht es hauptsächlich darum, die Merkmale zu identifizieren, die für die Zuordnung am erkennbarsten sind. Beispiele für die bekanntesten Klassifizierungsaufgaben sind:
- Die Kategorisierung einer E-Mail als Spam oder
Nicht-Spam. - Das Erkennen von Objekten in Bildern und Videos.
- Das Vorhersagen von potenziellen Gefahren im Bereich Versicherung und Finanzen.
Der Algorithmus
Der Algorithmus k-Nearest-Neighbor (KNN) ist ein Verfahren, mit dem neue Daten auf Basis von vorhandenen Daten klassifiziert werden können.k-Nearest-Neighbor ist einer der einfachsten Algorithmen zur Klassifizierung. Es werden zu einem neuen Datenpunkt die k nächsten Nachbarn bestimmt, wobei k eine beliebige natürliche Zahl darstellt. Der Algorithmus versucht, nahe liegende Datenpunkte herauszuziehen, um zu entscheiden, welche Klasse diesem Datenpunkt zugewiesen werden soll. Die Klasse, die unter k-Nachbarn am häufigsten vorkommt, wird die Klasse, zu der der neue Datenpunkt gehört.kkDas heißt, die Idee ist, dass der unbekannte Datenpunkt höchstwahrscheinlich in dieselbe Klasse fällt wie die bekannten Datenpunkte, denen er am ähnlichsten ist. Ein einfaches Beispiel: Sie sind auf einer Party und von den fünf Personen, die Ihnen am nächsten stehen, tragen drei einen Bart, also sind Sie wahrscheinlich auch Bartträger. Der k-Nearest-Neighbor-Algorithmus ist somit eine einfache mathematische Methode, um die Ähnlichkeit zwischen zwei Datenpunkten zu bestimmen. Bild 1 zeigt die Funktionsweise des k-Nearest Neighbor-Algorithmus.
Aufbau der Iris-Blüten (Bild 2)
Autor
Der Iris-Flower-Datensatz
Für das Klassifikationsbeispiel wird als Trainingsdatensatz das Iris-Flower-Dataset [1], das aus drei Arten von Schwertlilien mit je 50 Instanzen besteht, verwendet. Bild 2 zeigt die verschiedenen Iris-Blüten mit dem Kelchblatt (Sepal) und dem Kronblatt (Petal). Innerhalb des Iris-Flower-Datasets werden vier Merkmale gekennzeichnet: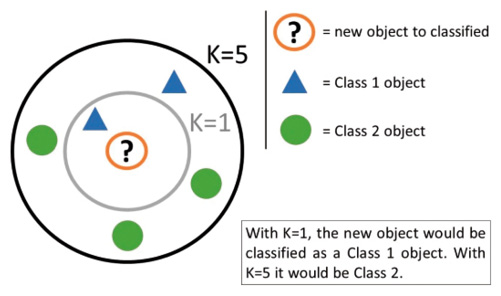
Funktionsweise des k-Nearest-Neighbor-Algorithmus (Bild 1)
Autor
- die Länge des Kelchblatts beziehungsweise Sepalum
(sepal.length), - die Breite des Sepalum (sepal.width),
- die Länge des Kronblatts beziehungsweise Petalum
(petal.length), - die Breite des Kronblatts (petal.width).
Trainings- und Testdatensatz
Die Trainingsdaten sind die Wissensbasis, mit der ein ML-Modell trainiert wird. Vereinfacht ausgedrückt handelt es sich um Beispiele, anhand derer ein Algorithmus lernt, eine bestimmte Datenkategorie zu erkennen.Testdaten werden verwendet, um die Leistung eines ML-Modells gegen unbekannte Daten zu prüfen beziehungsweise zu bewerten. Um das ML-Modell richtig trainieren zu können, ist es sinnvoll, die vorhandenen Daten in Trainings- und Testdaten zu unterteilen. In der ML-Terminologie bezeichnet man diesen Schritt als Splitting.Das heißt, um in der Testphase auf neue Datensätze zurückgreifen zu können, bedient man sich in der Praxis einer Art Kreuzvalidierung (Holdout), um die Daten nach einem Zufallsprinzip in zwei Teile aufzuteilen.Bei dieser Art der Validierung dient der Gesamtdatensatz für Training und Test. Zu den typischen Verhältnissen, die zur Aufteilung des Datensatzes verwendet werden, gehören 60:40 oder 80:20 Prozent. Der Trainingsdatensatz sollte aber auf jeden Fall immer größer als der Testdatensatz sein. Da im Beispiel der Iris-Datensatz nur sehr klein ist, hat sich dort in verschiedenen Versuchen eine Aufteilung von 70:30 als sehr gut erwiesen. Mit anderen Worten: Wir verwenden im Beispiel 70 Prozent (105 Datenpunkte) als Trainingssatz und die restlichen 30 Prozent (45 Datenpunkte) als Testsatz.Vorbereiten der Daten
Wie schon erläutert, besteht der Iris-Datensatz aus insgesamt 150 Sätzen mit jeweils 50 Einträgen mit vier Merkmalen. Bild 3 zeigt einen Ausschnitt der Tabelle iris.data in Excel.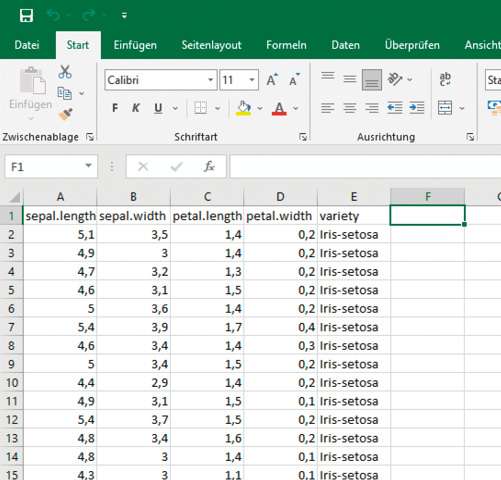
Aufbau der CSV-Datei Iris.Dataset (Bild 3)
Autor
Im ersten Schritt werden jetzt die Trainings- und Testdaten nach dem Zufallsprinzip ausgewählt. Fügen Sie hierfür dem Excel-Arbeitsblatt iris.data in den Spalten F, G und H die Spaltenüberschriften Random-Number, Rank und Set hinzu.Um jetzt die Trainings- und Testdatensätze zu unter-
scheiden, verwenden Sie die Funktion ZUFALLSZAHL(), um jedem Datensatz einen zufälligen Wert zwischen 0 und 1 zuzuweisen.Tragen Sie die Formel
scheiden, verwenden Sie die Funktion ZUFALLSZAHL(), um jedem Datensatz einen zufälligen Wert zwischen 0 und 1 zuzuweisen.Tragen Sie die Formel
=ZUFALLSZAHL()
in die Zelle F2 ein und vervollständigen Sie die Liste bis zum letzten Datensatz in Zeile F151.Da die Zufallszahl jetzt jedes Mal beim Ändern der Tabelle neu berechnet würde, kopieren Sie die erzeugten Zahlen einfach per [Strg]+[C] und fügen Sie diese über [Strg]+[Alt]+
[V] als feste Werte aus dem Dialogfenster in die Spalte ein.Im zweiten Schritt werden die Daten mithilfe der RANG.GLEICH()-Funktion in eine Reihenfolge von 1 bis 150
eingeteilt. Legen Sie somit in Spalte G2 (Rank) folgende Formel fest:
[V] als feste Werte aus dem Dialogfenster in die Spalte ein.Im zweiten Schritt werden die Daten mithilfe der RANG.GLEICH()-Funktion in eine Reihenfolge von 1 bis 150
eingeteilt. Legen Sie somit in Spalte G2 (Rank) folgende Formel fest:
=RANG.GLEICH(F2;$F$2:$F$151)
Ziehen Sie die Formel bis zum letzten Datensatz. Setzen Sie in Excel ein $-Zeichen vor den Bezug (Spalten- oder Zeilenbezug) innerhalb der Formel, so wird dieser Bezug beim Kopieren der Formel nicht angepasst. Das Kopieren erfolgt in diesen Fall mit absoluten Zellbezügen.Innerhalb der Zahlen von Spalte G entspricht der Rang einer Zahl ihrer Position in der Reihe, wenn die Zahlen nach Zahlenwerten aufsteigend oder absteigend sortiert sind. Hiermit haben Sie jetzt einen eindeutigen Wert für jeden Datensatz zwischen 1 und 150 erstellt. Über die vorgenommene Einteilung der Reihenfolge ist es jetzt möglich, die Datensätze in Trainings- und Testdatensätze aufzuteilen. Erstellen Sie hierfür in der Zelle H2 die Funktion:
=WENN(G2<=105;"Training";
"Test")
und füllen Sie die Zellen durch Ziehen mit der Maus bis zur Zelle H151 mit der Funktion aus.Die WENN()-Funktion ermöglicht es, einen Wert zurückzugeben, wenn eine Bedingung erfüllt ist, und einen anderen Wert, wenn die Bedingung nicht erfüllt ist. Die Funktion, WENN() bewirkt also, dass in Zelle H2 das Wort Training eingetragen wird, wenn G2 kleiner oder gleich 105 ist; ansonsten wird die Bezeichnung Test eingetragen.Markieren Sie die Überschriften und wählen Sie über die Schaltfläche Start | Sortieren und Filtern den Eintrag Filtern für die Spalten aus.Im nächsten Schritt können die Datensätze in zwei weitere Arbeitsblätter (Tabellenblätter) aufgeteilt werden.Erstellen Sie hierfür ein neues Arbeitsblatt (Tabelle) mit der Bezeichnung Trainingset und eine weitere Tabelle mit der Bezeichnung Testset. Filtern Sie jetzt die Daten nach Training und kopieren Sie diese Daten zusammen mit den Kopfzeilen (Spaltenüberschriften) und fügen Sie diese in das Tabellenblatt Trainingset ein. Verfahren Sie mit dem Arbeitsblatt Testset und den Testdatensätzen entsprechend.TrainingSind beide Arbeitsblätter erstellt, können Sie in diesen die Spalten F bis H entfernen. Fügen Sie noch jedem Tabellenblatt eine Spalte ID hinzu und vergeben Sie hier die Zahlen 1 bis 105 beziehungsweise 1 bis 45 für das Testset. Nutzen Sie hierfür einfach das automatische Ausfüllen der jeweiligen Spalte. Bild 4 zeigt den Ausschnitt aus dem Trainingset des Arbeitsblatts. Nachfolgend kann jetzt mit dem Aufbau des Models für den ML-Algorithmus begonnen werden.1105145
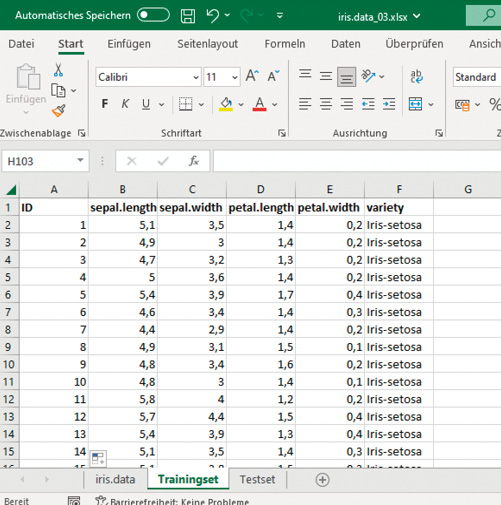
Aufbau des Trainingsets (Bild 4)
Autor
Das Modell
Die Daten für den Algorithmus sind erstellt und Sie können beginnen, das Modell aufzubauen. Das Modell für den KNN-Algorithmus stellt ein Verfahren dar, das konzeptuell am leichtesten mit Excel umzusetzen ist. Das Modell funktioniert, indem es den unbekannten Datenpunkt, der klassifiziert werden soll, mit seinen nächsten oder ähnlichsten Nachbarn vergleicht. Hier kommt die Methode des sogenannten überwachten Lernens zum Einsatz, da mit einer bereits vorhandenen Menge N von klassifizierten Datenpunkten gearbeitet wird.NDas heißt, für das Beispiel brauchen Sie nur jeden Punkt im Testset zu nehmen und seine Entfernung zu jedem Punkt im Trainingsetzuberechnen.Die Vorgabe ist also, man nimmt einen neuen, noch umklassifizierten Datenpunkt und misst einfach die Distanzen zu allen anderen Datenpunkten.Anschließend ordnen Sie die berechneten Distanzen absteigend nach Größe und wählen die k ersten Punkte mit der geringsten Distanz. Von diesen k Punkten bestimmen Sie die am häufigsten vorkommende Klasse und weisen diese dem neuen Datenpunkt zu.kkDie Berechnungsgrundlage der Distanz kann für den Algorithmus über die Definition der euklidischen Distanz (Abstand) geschaffen werden.Da jeder Datenpunkt M Merkmale hat, wird jeder Punkt, durch einen Vektor mit M Einträgen repräsentiert. Die euklidische Distanz zwischen zwei Vektoren a und b erhält man, indem man die Differenz zwischen den beiden Vektoren bildet und anschließend deren Länge beziehungsweise euklidische Norm berechnet. Bild 5 zeigt die allgemeine Formel für die euklidische Distanz [2].MMab
Formel für die euklidische Distanz (Bild 5)
Autor
Da diese Berechnungsgrundlage noch recht überschaubar ist, lässt sich ein Lösungsansatz sehr gut mit Excel erstellen. Der euklidische Abstand zwischen den Punkten q und p lässt sich bestimmen, indem jede Dimension für jeden Punkt genommen wird und die Differenz zwischen ihnen iterativ quadriert und die Differenzen addiert werden. In Excel können Sie über die Funktionen WURZEL, ZAHLENWERT und SVERWEIS eine entsprechende mathematische Lösung ausarbeiten.qp
Berechnung der Distanz
Nachdem geklärt ist, welche Berechnung notwendig ist, können Sie ein neues Arbeitsblatt (Tabelle) mit dem Namen Distanz anlegen.Für die Berechnung der Abstände wird eine 45 x 105-Matrix aufgebaut, um die einzelnen Distanzen zwischen den Datenpunkten im Testsatz und im Trainingsdatensatz abzubilden. In dem Beispiel entspricht jede Zeile einem Datenpunkt aus dem Tabellenblatt Testset und jede Spalte einen Datenpunkt aus der Tabelle Trainingset.TestsetTrainingsetErstellen Sie in dem neuen Arbeitsblatt Distanz eine Matrix ab Zelle A2 bis Zelle A46 mit einer Zahlenreihe von 1 bis 45. Nutzen Sie auch hier das automatische Ausfüllen von Excel. Tragen Sie dann in die Spalte B, Zelle B1, und dann quer (horizontal) bis zu Spalte DB1 die Zahlen 1 bis 105 ein.Distanz1451105Im nächsten Schritt wird für die Matrix eine Tabelle im Arbeitsblatt erstellt. Markieren Sie hierfür die gesamte Matrix (A1 bis DB46) und drücken Sie dann die Tastenkombination [STRG]+[T]. Aktivieren Sie das Häkchen Tabelle hat Überschriften (Bild 6) und klicken Sie auf Ok. Vergeben Sie jetzt noch in der Kopfzeile A1 die Überschrift Test-ID.A1DB46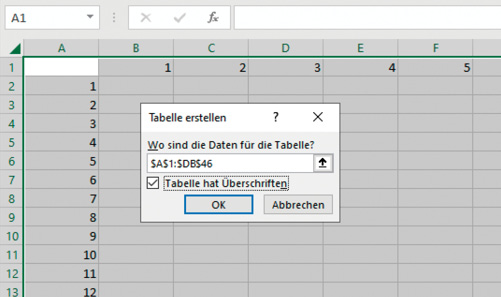
Definieren einer Tabelle im Arbeitsblatt (Bild 6)
Autor
Wenn Sie – wie in diesem Fall – eine Excel-Tabelle in einem Arbeitsblatt erstellen, weist die Tabellenkalkulation der Tabelle einen Namen zu.Wenn Sie der Excel-Tabelle dann Formeln hinzufügen, können diese Namen bei der Eingabe der Formel automatisch angezeigt werden, sodass Sie die Zellbezüge in der Tabelle auswählen können, statt sie manuell einzugeben.Diese Kombination aus Tabellen- und Spaltennamen wird als strukturierter Verweis bezeichnet. Die Namen im strukturierten Verweis passen sich beim Hinzufügen oder Entfernen von Daten in einer Tabelle an.Wir nutzen diese Möglichkeit für eine schnellere Formeleingabe bei der Berechnung der Distanz.Die Berechnung der Distanz beginnt in Zelle B2 der Tabelle. Es wird die Distanz zwischen dem ersten Punkt im Trainingset und dem ersten Punkt im Testset berechnet.Für die euklidische Distanzformel verwenden Sie die SVERWEIS-Funktion von Excel, um die Werte für jede Dimension zu finden und die Berechnung nach Bedarf durchzuführen. Die Formel zur Berechnung in Zelle B2 hat den nachfolgenden Aufbau:
=WURZEL(((SVERWEIS(ZAHLENWERT(Tabelle1[[#Kopfzeilen];
[1]]);Trainingset!$A$1:$F$106;2;FALSCH)-SVERWEIS(
Tabelle1[@[Test-ID]:[Test-ID]];Testset!$A$1:$F$46;2;
FALSCH))^2+(SVERWEIS(ZAHLENWERT(Tabelle1[[#Kopfzeilen];
[1]]);Trainingset!$A$1:$F$106;3;FALSCH)-SVERWEIS(
Tabelle1[@[Test-ID]:[Test-ID]];Testset!$A$1:$F$46;3;
FALSCH))^2+(SVERWEIS(ZAHLENWERT(Tabelle1[[#Kopfzeilen];
[1]]);Trainingset!$A$1:$F$106;4;FALSCH)-SVERWEIS(
Tabelle1[@[Test-ID]:[Test-ID]];Testset!$A$1:$F$46;4;
FALSCH))^2+(SVERWEIS(ZAHLENWERT(Tabelle1[[#Kopfzeilen];
[1]]);Trainingset!$A$1:$F$106;5;FALSCH)-SVERWEIS(
Tabelle1[@[Test-ID]:[Test-ID]];Testset!$A$1:$F$46;5;
FALSCH))^2))
Die WURZEL-Funktion gibt die benötigte Quadratwurzel einer Zahl zurück.Die Funktion SVERWEIS ermöglicht das Suchen beziehungsweise Nachschlagen in einer Tabelle. Die Funktion hat folgenden Aufbau:
=SVERWEIS(Suchkriterium;Matrix;Spaltenindex;
[Bereich_Verweis])
Der SVERWEIS steht für eine senkrechte Suche von oben nach unten. Für die waagerechte Suche steht alternativ der WVERWEIS zur Verfügung. Die Argumente in der Funktion beschreiben sich wie folgt:
- Suchkriterium: Steht für den Begriff, der gesucht wird.
- Matrix: Steht für den Bereich, in dem nach Informationen gesucht wird.
- Spaltenindex: Steht für die Spalte, in der sich die gesuchte Information befindet.
- [Bereich_Verweis]: Gibt an, ob mit genauer (FALSCH | 0) oder ungenauer (WAHR | 1) Übereinstimmung gesucht wird.
=ZAHLENWERT(Text;Dezimaltrennzeichen;
Gruppentrennzeichen)
wandelt den in Text angegebenen Inhalt in einen numerischen Wert um, und zwar unabhängig vom eingestellten Gebietsschema des Computers.Fertig ist die Distanzformel für die euklidische Distanz in Ihrer Excel-Tabelle. Bild 7 zeigt einen Ausschnitt des Arbeitsblatts nach dem Einsatz der Formel.
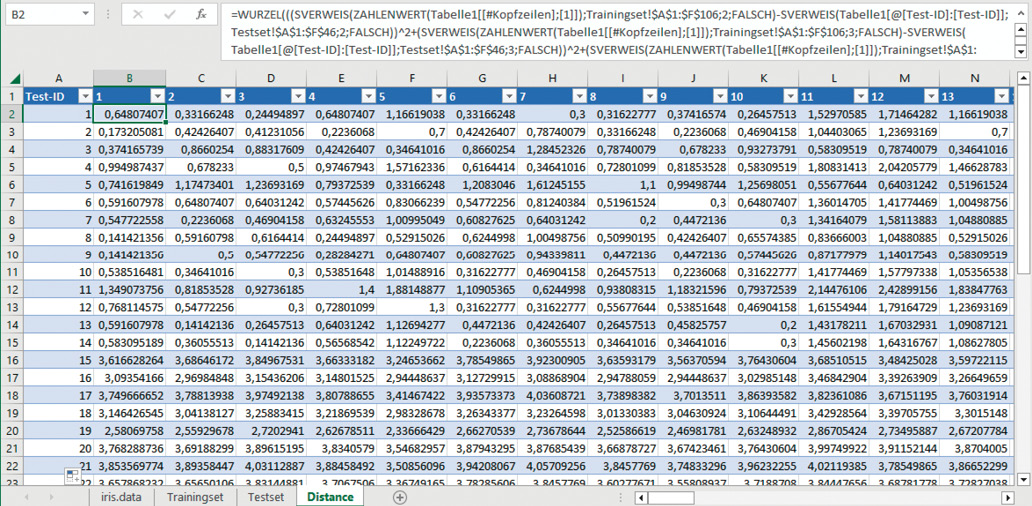
Die Berechnung der euklidischen Distanz (Bild 7)
Autor
k-Nearest-Neighbor
Nachdem Sie jetzt mithilfe der Formel den Abstand zwischen jedem Punkt in Ihrem Testdatensatz und jedem Punkt im Trainingset bestimmt haben, können Sie nun die nächsten Nachbarn (k-Nearest-Neighbor) zu jedem Punkt im Testset identifizieren.Um die Formel und das spätere Ergebnis noch übersichtlicher zu gestalten, beschränkt sich das Beispiel auf die Ermittlung der sechs nächsten Nachbarn aus dem Trainingset-Datensatz. Das heißt, Sie beginnen mit dem erstnächsten und dann mit dem zweitnächsten und so weiter. Der erstnächste Nachbar hat die kleinste Entfernung, der zweitnächste Nachbar hat die zweitkleinste Entfernung und so fort bis hin zum sechsten Nachbarn.Erstellen Sie für diese Aufgabe ein neues Arbeitsblatt mit der Bezeichnung k-Nearest-Neighbor. Füllen Sie die Spalte A mit den Ziffern 1 bis 45 beginnend ab A2 und vergeben Sie die Überschriften von Erster bis Sechster(Bild 8).A145ErsterSechster
Aufbau des Arbeitsblatts k-Nearest-Neighbor (Bild 8)
Autor
Als Berechnung müssen Sie jetzt den kleinsten Wert in der entsprechenden Zeile in der Distanztabelle identifizieren, die Spaltennummer für diesen gesuchten Wert ermitteln und dann den Namen zurückgeben, den Sie durch die ID des Wertes im Trainingset erhalten haben.Erreicht wird diese Berechnung über eine Kombination der Funktion INDEX() und VERGLEICH(). Die Formel hat für den k-Nearest-Neighbor folgenden Aufbau:
=SVERWEIS(ZAHLENWERT(INDEX(
Tabelle1[#Kopfzeilen];VERGLEICH(KKLEINSTE(
Distanz!$B2:$DB2;1);Distanz!2:2;FALSCH)));
Trainingset!$A$1:$F$106;6;FALSCH)
Die Funktion SVERWEIS ist ja schon bekannt, INDEX(Matrix; Zeile; [Spalte]) gibt den Wert eines Elements in einer Tabelle oder einem Array zurück, ausgewählt anhand der Zeilen- und Spaltennummernindizes. Mit der Funktion VERGLEICH(Suchkriterium; Suchmatrix; [Vergleichstyp]) wird in einem Bereich von Zellen nach einem angegebenen Element gesucht und anschließend die relative Position dieses Elements im Bereich zurückgegeben.Ziehen Sie die Formel von Zelle B2 bis zu Zelle B46. Hiermit haben Sie jetzt Ihren ersten Nachbarn bestimmt.Für die nachfolgenden Berechnungen müssen Sie den Wert (Bild 9) in der Funktion KKLEINSTE() manuell anpassen, um den gesuchten Nachbarn (2, 3, 4, 5 und 6) zu identifizieren. Die Funktion KKLEINSTE(Matrix;k) gibt den k-kleinsten Wert einer Datengruppe zurück. Mit dieser Funktion können Sie Werte ermitteln, die innerhalb einer Datenmenge eine bestimmte relative Größe haben. Bild 10 zeigt das erstellte Arbeitsblatt k-Nearest-Neighbor.KKLEINSTE()k-Nearest-Neighbor
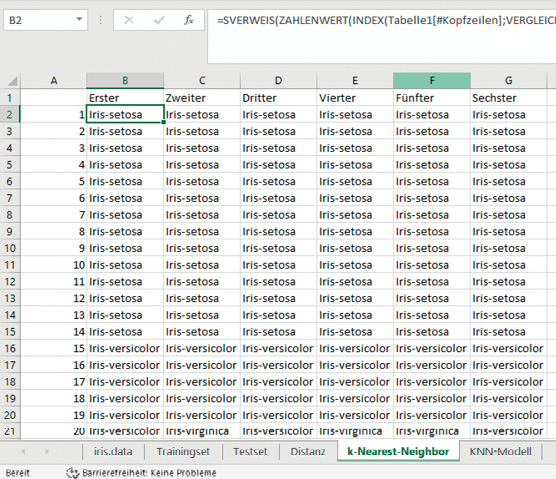
Das fertige Arbeitsblatt k-Nearest-Neighbor (Bild 10)
Autor
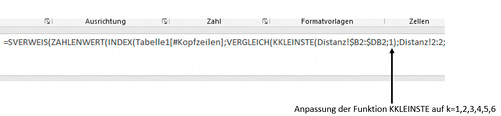
Anpassung der Funktion KKLEINSTE (Bild 9)
Autor
Auswertung des KNN-Modells
In der letzten Phase der Beispielanwendung wird nun ein Formel-Algorithmus entwickelt, um den optimalen k-Wert zu bestimmen. Dabei soll es möglich sein, verschiedene k-Werte (1 bis 6) auszuprobieren und die Fehlerrate für jeden einzelnen mit den Testset-Datensätzen zu berechnen und denjenigen Wert zurückzugeben, der die niedrigste Fehlerrate erzeugt. Erstellen Sie ein neues Arbeitsblatt mit der Bezeichnung KNN-Modell wie im Bild 11 dargestellt. Die Testdatenpunkte in Spalte A sind mit 1 bis 45 angegeben.KNN-Modell145
Aufbau des Arbeitsblatts KNN-Modell (Bild 11)
Autor
Als Erstes soll in der neuen Tabelle der Vorhersagewert für den angegebenen k-Wert in Zelle B1 ermittelt werden. Für den Fall, dass der gesuchte k-Wert einfach 1 wäre, könnte man den nächsten Nachbarn allein über =’k-Nearest-Neighbor’!B2 bestimmen. Allerdings würde das schon nicht mehr funktionieren, wenn k>1 ist. Daher muss der Algorithmus entsprechend erweitert werden.B11k>1Im Beispiel wird die WENNFEHLER()-Funktion von Excel verwendet. Diese Funktion gibt einen Fehler zurück, wenn es zwei Nachbarn gibt, die für den angegebenen k-Wert in Zelle B1 gleich oft vorkommen. Die Formel des Algorithmus zur Berechnung der Vorhersage von k (1 bis 6) sieht wie folgt aus:
=WENNS($B$1=1;'k-Nearest-Neighbor'!B2;$B$1=2;WENNFEHLER(
INDEX('k-Nearest-Neighbor'!B2:C2;MODALWERT(VERGLEICH(
'k-Nearest-Neighbor'!B2:C2;'k-Nearest-Neighbor'!B2:C2;0
)));'k-Nearest-Neighbor'!B2);$B$1=3;WENNFEHLER(INDEX(
'k-Nearest-Neighbor'!B2:D2;MODALWERT(VERGLEICH(
'k-Nearest-Neighbor'!B2:D2;'k-Nearest-Neighbor'!B2:D2;0
)));'k-Nearest-Neighbor'!B2);$B$1=4;WENNFEHLER(INDEX(
'k-Nearest-Neighbor'!B2:E2;MODALWERT(VERGLEICH(
'k-Nearest-Neighbor'!B2:E2;'k-Nearest-Neighbor'!B2:E2;0
)));'k-Nearest-Neighbor'!B2);$B$1=5;WENNFEHLER(INDEX(
'k-Nearest-Neighbor'!B2:F2;MODALWERT(VERGLEICH(
'k-Nearest-Neighbor'!B2:F2;'k-Nearest-Neighbor'!B2:F2;0
)));'k-Nearest-Neighbor'!B2);$B$1=6;WENNFEHLER(INDEX(
'k-Nearest-Neighbor'!B2:G2;MODALWERT(VERGLEICH(
'k-Nearest-Neighbor'!B2:G2;'k-Nearest-Neighbor'!B2:G2;0
)));'k-Nearest-Neighbor'!B2))
Die Funktion MODALWERT(Zahl1; [Zahl2]; ...) gibt den am häufigsten vorkommenden (wiederholten) Wert in einem Array oder Datenbereich zurück.Die Funktion WENNS(...) überprüft, ob eine oder mehrere Bedingungen erfüllt sind, und gibt einen Wert zurück, der der ersten TRUE-Bedingung entspricht. Die WENNS-Funktion in Excel kann bis zu 127 verschiedene Bedingungen testen. Im nächsten Schritt soll die bekannte Klassifizierung jedes Testpunkts abgerufen werden, um festzustellen zu können, ob die Vorhersage richtig war oder nicht. Dazu verwenden Sie wieder die SVERWEIS(...)-Funktion von Excel:
=SVERWEIS(A4;Testset!$A$1:$F$46;6;FALSCH)
In der Spalte D (Fehler) wird die Vorhersage mit dem tatsächlichen Wert verglichen und eine 1 zurückgegeben, wenn die Vorhersage fehlerhaft war. Bestimmt wird das Ganze über eine WENN(...)-Funktion:1
=WENN(B4=C4;0;1)
Als Letztes berechnen Sie in Zelle B2 die Fehlerrate wie folgt:B2
=SUMME(D4:D48)/ANZAHL(D4:D48)
Hier wird einfach die Anzahl der Fehler durch die Gesamtzahl der Datenpunkte dividiert.Fertig ist der k-Nearest-Neighbor-Algorithmus nur mithilfe von Excel-Funktionen. Sie können die verschiedenen k-Werte von 1 bis 6 ausführen und das Modell auswerten. Eine erneute Berechnung der Tabelle erzwingen Sie über die Tastenkombination [Strg]+[Alt]+[F9].
Modellauswertung
Wie Sie bei der Auswertung des Modells festgestellt haben werden, fallen die meisten oder fast alle Datenpunkte für die sechs nächsten Nachbarn alle in dieselbe Klassifizierung.Das Ergebnis ist sehr stark abhängig von dem verwendeten Datensatz. Der Iris-Datensatz ist so konzipiert, dass dieser durch die Clusterung sehr einfach zu handhaben ist und es sich des Weiteren um einen niedrigdimensionalen Datensatz mit nur vier Dimensionen handelt. Wenn Sie mit realen beziehungsweise großen Datenmengen arbeiten, werden Sie feststellen, dass diese weitaus weniger geclustert sind, insbesondere wenn die Anzahl der Dimensionen zunimmt. Je weniger Daten geclustert sind, desto größer muss der Trainingssatz sein, um ein nützliches Modell zu erstellen.Fazit
Machine Learning ist inzwischen in allen Bereichen der IT angekommen. In diesem Artikel haben Sie erfahren, dass man auch ohne Programmierung einfache ML-Lösungen zur Analyse mit Excel ausführen kann. Eine sinnvolle Erweiterung beispielsweise durch VBA kann Ihnen die Arbeit und die Analyse von Daten sehr stark erleichtern. Auch eine Umsetzung von Excel-Formeln beziehungsweise erstellten Algorithmen auf eine andere Programmiersprache kann als Übungs- oder Lehraufgabe sehr nützlich sein.Fussnoten
- Iris Data Download, http://www.dotnetpro.de/SL2401MLExcel1
- Euklidischer Abstand, http://www.dotnetpro.de/SL2401MLExcel2