18. Jul 2022
Lesedauer 14 Min.
Eine gute Lösung finden
Methoden des Operations Research, Teil 1
Wer komplexe Probleme lösen muss, findet in den Google OR-Tools wertvolle Werkzeuge.
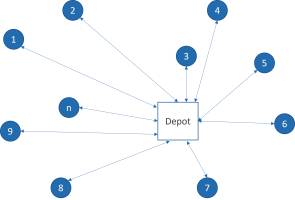
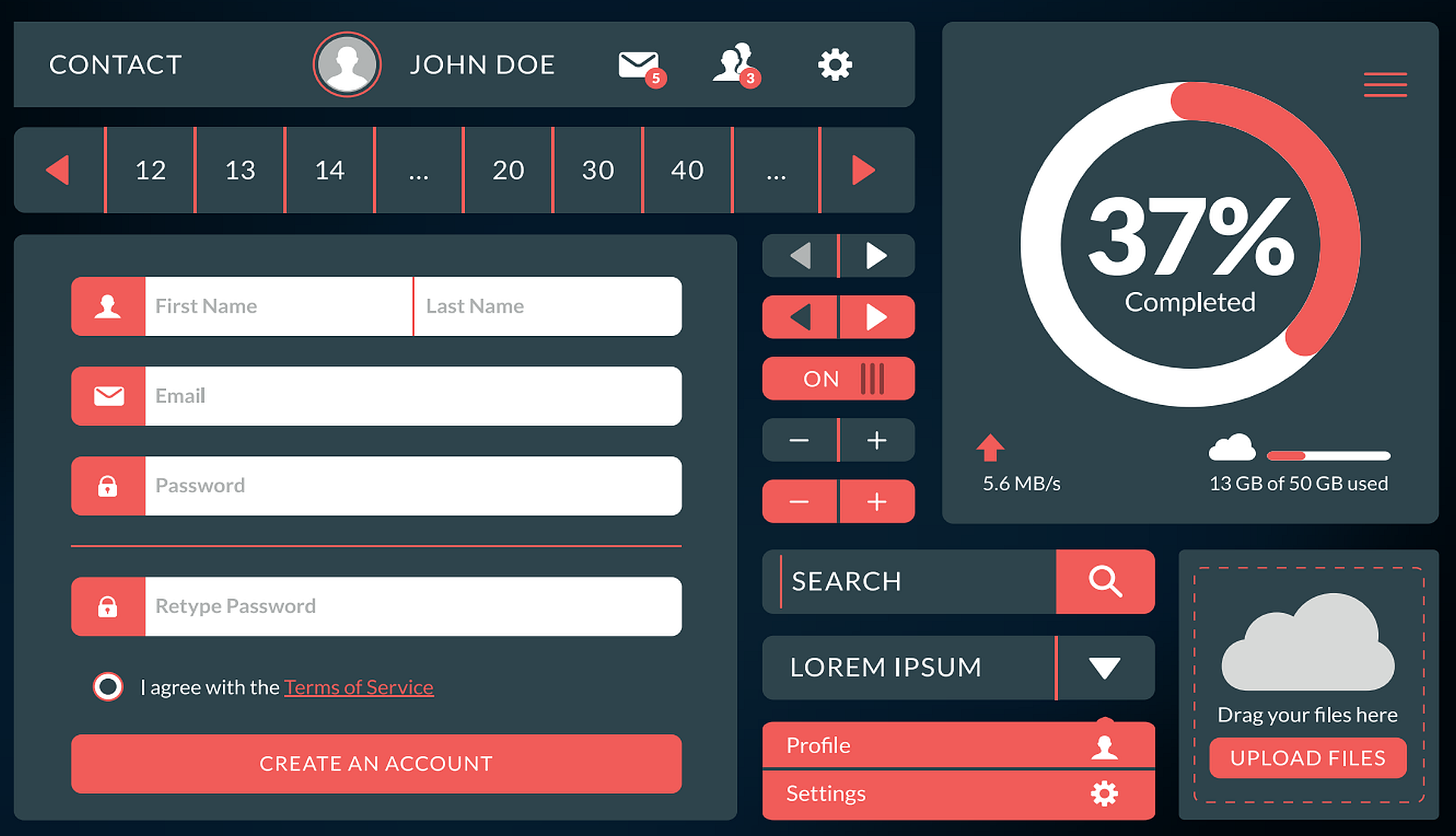
Aus dem zentralen Lager müssen 500 Ladungen zu Kunden gebracht werden. Dabei sind Kapazitätsgrenzen der Fahrzeuge genauso zu beachten wie mögliche Lieferzeitfenster. Es sind die üblichen Fragen des Tagesgeschäfts, die sich dabei stellen: Welche Ladungen sollen auf welchen Lkw und welche Reihenfolge sollen die Fahrer bei der Anfahrt wählen? Und wie muss umgeplant werden, wenn Sendung Nummer 47 doch später zugestellt werden muss als gedacht?Derartige Probleme sind typisch für die betriebliche Entscheidungspraxis. Dabei ist das skizzierte Tourenplanungsproblem ein bekanntes Beispiel aus einer Reihe von sogenannten Optimierungsproblemen. Dazu gehören beispielsweise Fragen aus dem Bereich der Beladung und Verpackung, der Personaleinsatzplanung, der Verkehrsplanung und so weiter.Mit Blick in die Wissenschaft handelt es sich dabei um Optimierungsprobleme. Was ist darunter zu verstehen? Ein Optimierungsproblem beschreibt eine mathematische Aufgabe, bei der es in der Regel darum geht, unter bestimmten Bedingungen einen bestmöglichen Wert – das Optimum – einer Zielfunktion zu bestimmen. Bei diesem Optimum handelt es sich sehr oft um einen Minimal- oder einen Maximalwert. Konkret: Das Transportproblem mit den 500 auszuliefernden Frachten bei Beachtung der Lieferzeitfenster ließe sich im Extremfall mit 500 Lkw lösen. Dabei bedient jeder Lastkraftwagen genau einen Auftrag und erfüllt diesen.Es dürfte schnell klar sein, dass diese Lösung nicht wirklich brauchbar oder gut sein kann (Bild 1). Die Anzahl der Lkw ist viel zu hoch und die gefahrenen Strecken sind zu groß. Dennoch wäre diese Lösung gültig, jedoch weit entfernt von einem guten Ergebnis. Es handelt sich um eine Ausgangslösung, die zu verbessern ist.
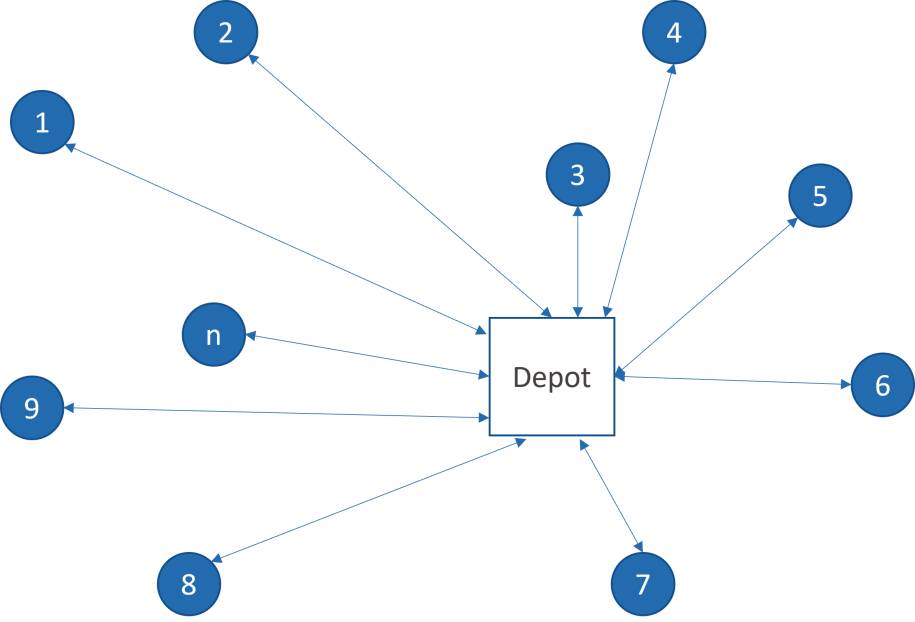
Ausgangslösung:Für jeden Auftrag ein Lkw ist wenig optimal(Bild 1)
Autor
Machen wir daraus ein Optimierungsproblem: Gesucht ist die optimale Aufteilung der Frachten auf einzelne Lkw, sodass die zu fahrende Gesamtstrecke und damit auch die anfallenden Kosten minimal werden. Das ist so weit verständlich. Kann man nun die Lösung nicht ausrechnen oder durch systematisches Probieren ermitteln? Das kann man. Die Fragen sind dabei:
- Welches Verfahren kommt in Frage?
- Wie lange würde es dauern, eine oder mehrere Lösungen zu finden?
- Welche Güte/Qualität hat die Lösung?
- Planen des Produktionsprogramms,
- Ermitteln des Materialbedarfs,
- Festlegen von Losgrößen und Kapazitäten in der Produktion,
- Personaleinsatzplanung,
- Planen von Wartung und Instandhaltung,
- Fahrzeugrouting.
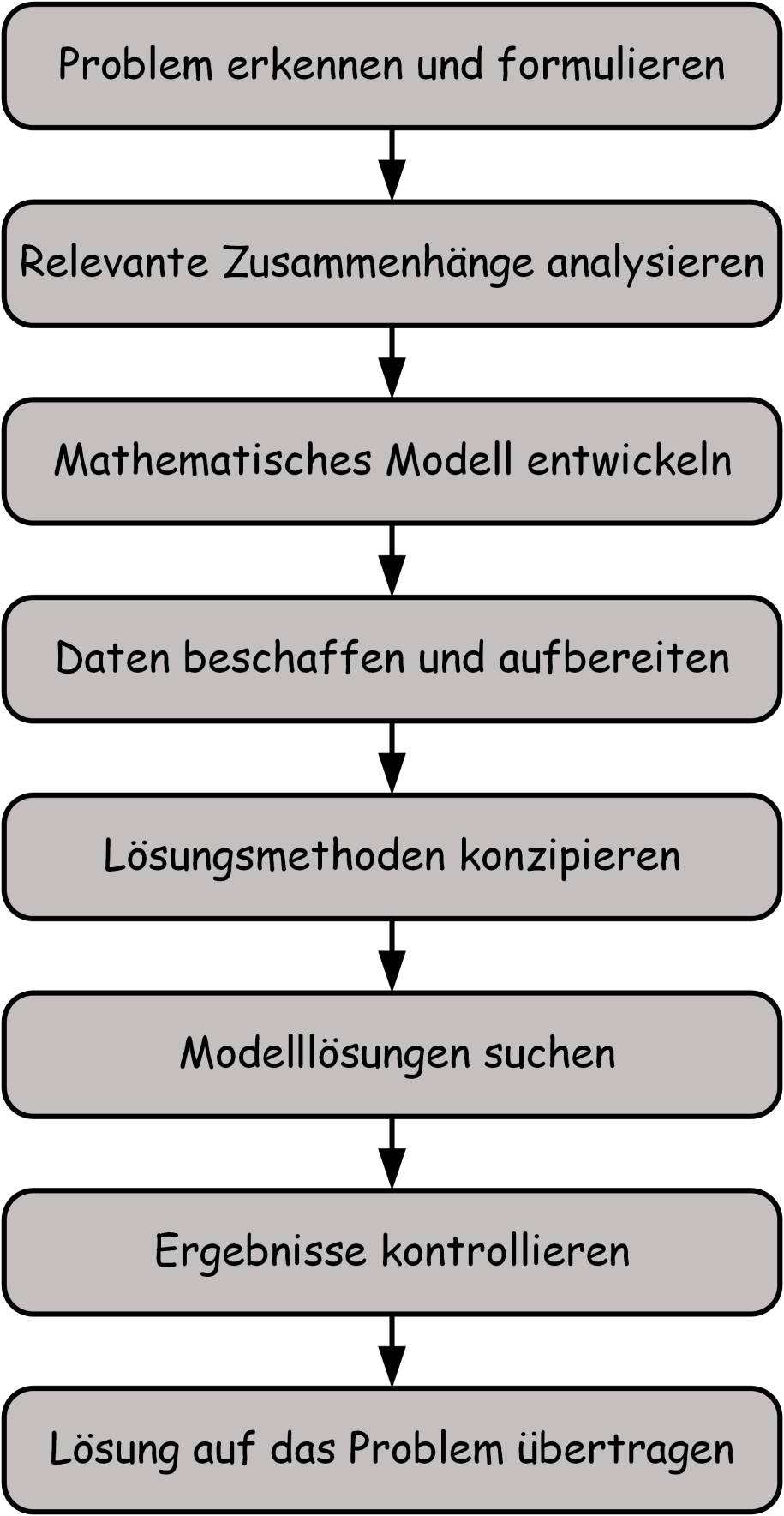
Schrittezur Anwendung von OR für komplexe Probleme(Bild 2)
Autor
Das Problem muss also aus dem betrieblichen Kontext in ein Lösungsmodell überführt werden. Diesem Lösungsmodell liegen unterschiedliche Lösungsverfahren zugrunde. Dazu gehören zum Beispiel Simulationsverfahren, graphenbasierte Verfahren oder Modelle der Spieltheorie. Auch heuristische Verfahren und Entscheidungsbaumverfahren kommen zum Einsatz.Ein Beispiel: Die Warteschlangentheorie lässt sich erfolgreich bei der Planung einer Service-Hotline einsetzen. Mithilfe von Optimierungsverfahren kann ausgehend von Warteschlangenmodellen auf die wirtschaftlichsten Kapazitäten eines Callcenters geschlossen werden. Die wichtigsten Ausgangsgrößen sind in diesem Fall die angestrebte mittlere Bedienzeit, das erwartete Anrufaufkommen sowie die angestrebte Servicequalität. Es gibt mehrere Ansätze, die hauptsächlich aufgrund unterschiedlicher Ausgangsmodelle zustande kommen [2].
Problem des Handlungsreisenden
Bei diesem Problem geht es darum, die beste Tour für einen Besuch von Kunden in mehreren Städten zu planen. Dabei soll keine Stadt mehrmals besucht werden, es soll die kürzeste Strecke ausgesucht werden und der Handlungsreisende soll am Ende wieder in seiner Stadt ankommen. Es geht also um eine Rundreise.
Das angeführte Problem der Tourenplanung aus der Praxis für die Zuordnung der Ladungen auf die Lkw beruht im Kern auf dem bekannten Problem des Handlungsreisenden, das der gleichnamige Kasten erläutert. Hat man eine Lösung für das Modell gefunden, ist diese durch Interpretation und Übersetzung auf die reale Frage zurückzuführen (Bild 3).
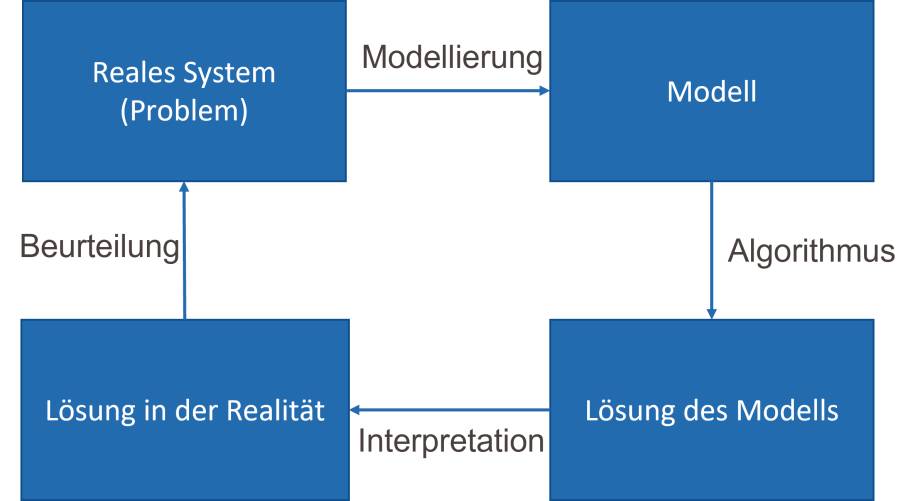
Zusammenhang:Realität und Modell(Bild 3)
Autor
Der entwickelte Algorithmus muss dann in Software überführt werden. Neben der Eigenimplementierung gibt es auch interessante Bibliotheken. Eine solche Bibliothek sind die Google OR-Tools [3], die das Thema dieser zweiteiligen Artikelfolge sind.
Google OR-Tools
Die Google OR-Tools sind Open Source und stellen Algorithmen zur kombinatorischen Optimierung als Bibliotheken zur Verfügung, geschrieben in C++. Gemäß der Dokumentation lassen sich die Bibliotheken in Projekten mit den Programmiersprachen C++, Python, Java oder C# (.NET) einsetzen. Die Google OR-Tools bieten Algorithmen aus den folgenden Bereichen:- lineare Optimierung (linear optimization),
- ganzzahlige Optimierung (integer optimization),
- Optimierung mit Beschränkungen
(constraint optimization), - Routingprobleme (routing),
- Zuordnungsprobleme (bin packing),
- Netzwerkflüsse (network flows),
- Terminplanung (scheduling).
Lineare Optimierung
Die lineare Optimierung oder auch lineare Programmierung (LP) ist eines der Hauptverfahren des Operations Research, das in vielen Bereichen zum Einsatz kommt. Dabei gibt es eine Zielfunktion, die einen linearen Zusammenhang aufweist, und es gibt eine Reihe von Nebenbedingungen. Diese wiederum können als Gleichung oder Ungleichung vorliegen. Das Ziel besteht dann in einer Minimierung oder Maximierung des Zielfunktionswerts. Es gibt beispielsweise die folgenden Anwendungen mit Praxisbezug:- Produktionsplanung: Zusammenstellung eines Produktionsprogramms, das bei gegebenen Verkaufspreisen und Kosten der Materialien zu einem maximalen Gewinn führt. Das ist dann der Fall, wenn ein Unternehmen verschiedene Produkte herstellt und für die Herstellung jeweils eine bestimmte Menge an Ressourcen benötigt. Anhand der linearen Optimierung wird die ideale Produktionsmenge, das heißt die gewinnmaximale Menge der jeweiligen Güter herausgefunden.
- Routing in Telekommunikations- und Verkehrsnetzen: Hier wird die lineare Optimierung oft in Verbindung mit einer Kapazitätsplanung eingesetzt, um die Verkehrsflüsse so zu führen, dass die Verkehrsanforderungen unter Berücksichtigung der Kapazitätsbedingungen erfüllt sind. Dabei sind zum Beispiel bei einem öffentlichen Straßenbahnnetz alle Haltestellen in einer bestimmten Frequenz zu bedienen (Nebenbedingung) und die gefahrene Entfernung ist zu minimieren (Zielfunktion).
- Mischungsprobleme: Es geht um die Bestimmung der Zusammensetzung von Zutaten zu einem Endprodukt. Die Menge der Zutaten variiert dabei in einem bestimmten Bereich. Ein bekanntes Diätproblem kann als Beispiel dienen. Es sind eine Reihe von Produkten mit ihrem Gehalt an bestimmten Nährwerten und ihrem Preis pro Kilogramm gegeben. Die Herausforderung besteht in der Mischung aus den Rohmaterialien von einem oder mehreren Endprodukten zu minimalen Kosten unter der Nebenbedingung, dass bestimmte Mindest- und Höchstgrenzen für die einzelnen Nährwerte eingehalten werden. Ob die automatisch generierten Malzeiten dann noch schmackhaft sind, ist eine andere Frage.
- MPSolver,
- Linear Optimization Service in Google Apps Script.
Ganzzahlige Optimierung
Die ganzzahlige Optimierung eignet sich zum Lösen von Problemen des praktischen Lebens, für die keine speziellen Algorithmen bekannt sind; also zum Beispiel Probleme der Produktionsplanung, bei der Dienst und Umlaufplanung, bei der Kapazitäts- und Routenplanung für Telekommunikationsnetze und bei der Tourenplanung. Bei der sogenannten 0/1-Programmierung handelt es sich um einen Spezialfall der ganzzahligen Optimierung, bei dem die Variablen auf die binären Werte 0 oder 1 beschränkt sind.Die Google OR-Tools bieten zur Lösung von ganzzahligen Optimierungsproblemen folgende Möglichkeiten:- MPSolver,
- CP-SAT Solver,
- Original CP Solver.
Zuordnungsprobleme
Zuordnungsprobleme gehören zu den bekanntesten kombinatorischen Optimierungsproblemen. Eine Problemstellung könnte in diesem Fall wie folgt lauten: Angenommen, eine Gruppe von Arbeitskräften muss eine Reihe von Aufgaben ausführen und für jede Arbeitskraft und Aufgabe fallen Kosten für die Zuweisung der Arbeitskraft an die Aufgabe an. Das Problem besteht darin, jedem Arbeiter höchstens eine Aufgabe zuzuweisen, ohne dass zwei Arbeiter dieselbe Aufgabe ausführen, und gleichzeitig sollen die Gesamtkosten minimal werden. Eine Aufgabe entspricht einer Teilmenge der Kanten, in denen jeder Arbeiter höchstens eine Kante hat und von zwei Arbeitern keine Kanten starten, die zu derselben Aufgabe führen. Problem und Lösung (Zuordnung) sind in Bild 4 dargestellt [3].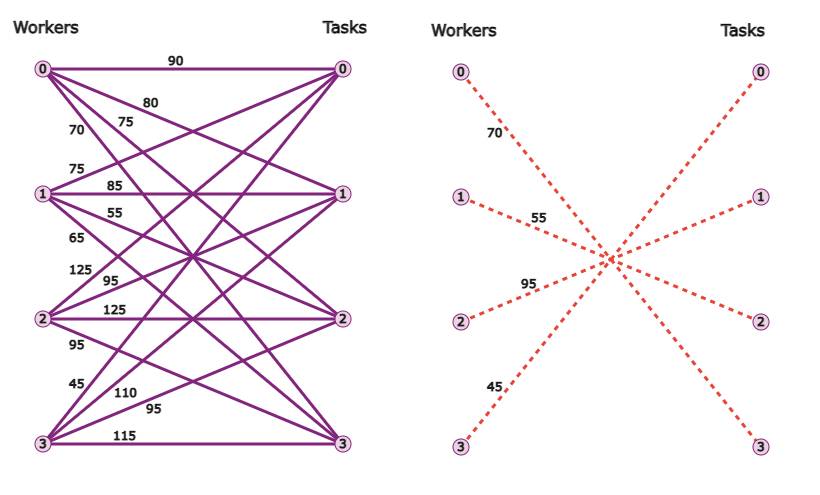
Arbeiter und Aufgaben:Beispiel für ein Zuordnungsproblem(Bild 4)
Autor
Auch spezielle Transportprobleme gehören in diese Kategorie. Gemeint sind Fragestellungen, die nach der kostenoptimalen Zuordnung von Sachen, Personen oder Betriebsmitteln zu bestimmten Orten, Stellen oder Aufgaben suchen.MPSolver und CP-SAT Solver lassen sich einsetzen, um derartige Zuordnungsprobleme zu lösen.
Network Flows
Bei Network Flows geht es um die Netzwerkoptimierung, das heißt um Lösung von Problemen, deren Struktur anhand von Graphen und Netzwerkflüssen dargestellt werden können. Network Flows setzten sich aus Knoten und Verbindungen zwischen diesen Knoten, den Kanten, zusammen. Auch diese Modelle können Logistikprobleme zwischen Standorten (Knoten) über Verkehrsverbindungen (Kanten) darstellen.Eine wichtige Einschränkung ist, dass die Kapazität der Kanten, das heißt die Menge an Gütern, die hierüber transportiert werden können, beschränkt ist. Beim bekannten Maximum-Flow-Problem ist die maximale Gesamtmenge zu bestimmen, die über alle Kanten im Netzwerk transportiert werden kann. Dabei sind die Kapazitätsbeschränkungen der Kanten zu beachten.Network Flows eignen sich somit, viele praxisorientierte Probleme zu lösen, beispielsweise zum Optimieren von Transport-, Fluss- und Distributionsmodellen und zum Planen von Versorgungsnetzen, Touren und Standorten. Nachfolgend werden einige weitere Problemstellungen erläutert.Eine interessante Frage ist das sogenannte Briefträgerproblem: Ein Briefträger soll die Häuser eines bestimmten Stadtteils mit Post beliefern. Network Flows können eingesetzt werden, um dafür einen geschlossenen Weg von minimaler Länge zu bestimmen. Der Weg soll jede zu bedienende Straße mindestens einmal enthalten. Die Länge der unproduktiven Strecken soll dabei minimiert werden.Personaleinsatzplanung
Die Personaleinsatzplanung gehört zu den Optimierungsproblemen und kann somit dem Themenfeld des Operations Research zugeordnet werden. Bei der Personaleinsatzplanung geht es um das Einsetzen von Mitarbeitern an verschiedenen Positionen unter Berücksichtigung von Qualifikationen und zeitlichen Aspekten. Eine gute Personaleinsatzplanung soll eine höhere Produktivität und reibungslose Abläufe sicherstellen. Auch die Schichtplanung fällt darunter. Es geht darum, dass die Planung mehrere Schichten erforderlich ist, unter Berücksichtigung komplexer Einschränkungen und Personalanforderungen, zum Beispiel in einem Krankenhaus. Dabei sollen für jede Schicht genügend Arbeitskräfte eingeplant werden und kein Mitarbeiter soll zwei Schichten hintereinander arbeiten.Einen solchen Schichtplan zu erstellen, der alle Einschränkungen erfüllt, kann rechnerisch sehr anspruchsvoll sein. Als Beispiel kann das Erstellen der Personaleinsatzplanung für drei Tage und für vier Mitarbeiter des Pflegepersonals eines Krankenhauses dienen. Jeder Tag ist dabei in Acht-Stunden-Schichten unterteilt und eine Schicht wird einer Person zugewiesen. Wichtig ist dabei, dass keine Person mehr als eine Schicht am Tag arbeitet. Innerhalb von drei Tagen soll jede Person mindestens zwei Schichten übernehmen. Google bietet für die Lösung solcher Probleme die Nutzung des CP-SAT Solver an.Packungsprobleme
Die bekannten Fragen aus diesem Bereich sind das sogenannte Rucksack- oder Knapsack-Problem und das Bin-Packing-Problem. Das Rucksack-Problem gehört zu den kombinatorischen Optimierungsproblemen. Hier geht es darum, eine Auswahl von Artikeln, die ein bestimmtes Volumen, Gewicht und Nutzwert aufweisen, in einen Behälter mit einem festen Fassungsvermögen zu packen. Dabei soll die Summe des Nutzwerts der ausgewählten Produkte maximiert werden.Beim Bin-Packing oder auch Behälterproblem ist eine Anzahl an Behältern mit einer vorgegebenen Größe und eine bestimmte Anzahl an Objekten mit einer bestimmten Größe und Gewicht gegeben. Die Frage lautet nun wie folgt: Wie lassen sich die gegebenen Objekte so auf die Behälter verteilen, dass keiner überläuft?Interessant ist das Auffinden einer Zuordnung, bei der die Anzahl an Behältern minimiert wird. Es handelt sich lediglich um eine allgemeine Formulierung, die sich variieren lässt. In der Praxis der Verpackungsindustrie spielt der Bin-Packing-Algorithmus eine wichtige Rolle.Verkehrsplanung
Eine der wichtigsten Anwendungen des Operations Research ist die Routenplanung für Fahrzeuge. Der Anfang des Artikels hat ja schon ein Beispiel geschildet und den Basisalgorithmus des Handlungsreisenden vorgestellt. Das Ziel ist in der Regel, die „beste“ Route für eine Flotte von Fahrzeugen zu finden. Als beste Route wird diejenige angesehen, welche die geringste Gesamtentfernung oder die geringsten Kosten aufweist. Erschwerend werden dann weitere Bedingungen in das Problem aufgenommen, zum Beispiel:- Zeitfenster für Be- und Entladung,
- maximale Kapazitäten der Fahrzeuge,
- Veränderungen bei der Auftragslage während der Ausführung, zum Beispiel kommen weitere Aufträge hinzu.
Weitere Anwendungsgebiete des OR
Anhand der genannten Beispiele konnten Sie bereits eine Vielzahl von interessanten Anwendungsbereichen erkennen. Darüber hinaus finden die Methoden des OR auch bei den folgenden Fragen Anwendung:- Logistik: Optimales Beladen von Schiffen und Lkw, Planung von Paketverteilzentren.
- Anlagenplanung: Planen der Aufstellung und Dimensionierung von Maschinen, Strukturierung oder Umstrukturierung von Fabriken.
- Personalplanung: Prognose der Auswirkungen, wenn Mitarbeiter der Belegschaft altersbedingt ausscheiden. Auf diese Weise lässt sich besser planen, wann welche Nachwuchskräfte eingestellt werden sollten und welche Fortbildungsmaßnahmen notwendig sind.
- Verkehr: Planen von Verkehrswegen, Reaktion auf Störungen wie Zugausfälle oder Verspätungen.
- Finanzwesen: Ausarbeiten von Anlage- und Investitionsstrategien.
- Produktion: Anwendung bei der Bestimmung von Rohstoffmengen, bei der Planung der auszubringenden Mengen sowie bei der Festlegung der Maschinenauslastung.
Anwendung der Google OR-Tools
Konkrete Beispiele wird der zweite Teil der Serie vorstellen. Hier folgen zunächst einige Hinweise zur Installation der OR-Tools von Google.Für .NET (C#) stehen kompilierte Binärdateien sowie der komplette Quellcode zur Verfügung, aus dem sich ein aktueller Build erzeugen lässt. Die Dokumentation nennt folgende technische Vorgaben:- Windows 10 64-Bit,
- Visual Studio 2019/2022,
- Microsoft Visual C++ Redistributable; wählen Sie die x64-Version; diese ist notwendig, da die OR-Tools-Bibliothek für .NET ein Wrapper für die native C++-Bibliothek ist,
- .NET Core 2.1 SDK.
Fazit und Ausblick
Moderne Software jenseits einer schnöden Daten- und Dateiverwaltung kann mit innovativer Funktionalität glänzen, die auf ausgeklügelten Algorithmen beruht. Komplexe Berechnungen oder Suchverfahren nach einer guten – nicht unbedingt der optimalen – Lösung müssen nicht auf künstlicher Intelligenz basieren, sondern auf etablierten Algorithmen und Heuristiken. Diese Verfahren bringen bei großer Rechenpower Lösungen hervor, die sich manuell nicht in akzeptabler Zeit ergeben würden. Tourenpläne für Speditionen oder optimierte Dienstpläne für die Schichtarbeit entstehen dann auf den sprichwörtlichen Knopfdruck hin.Mithilfe dieser Algorithmen können Sie bestimmte Funktionen in Software deutlich erweitern, verbessern oder auch erst möglich machen. Die Verfahren dazu sind nicht neu. Dennoch ist es komplex, diese Algorithmen von Grund auf neu zu entwerfen und zu implementieren. Aber das müssen Sie auch nicht. Bibliotheken und Frameworks wie die OR-Tools von Google machen die Verwendung deutlich einfacher.Der zweite Teil der Serie wird sich dann dem Einsatz der OR-Tools von Google anhand von konkreten Beispielen mit C# und .NET widmen.Fussnoten
- Operations Research (OR),
- Henner Graubitz, Entwicklung eines Forecastsystems für Call Center mit Best Service Routing,
- Google OR-Tools,