Deep Learning mit Python
Python und AI, Teil 3

Dieser Beitrag führt zunächst in die Grundlagen neuronaler Netze ein und vergleicht anschließend TensorFlow und PyTorch. Danach wird exemplarisch gezeigt, wie man mit TensorFlow/Keras ein einfaches Modell zur Bildklassifikation erstellt, trainiert und optimiert.
Künstliche neuronale Netze bilden das Fundament moderner Künstlicher Intelligenz und sind das zentrale Konzept des Deep Learning. Inspiriert vom Aufbau des menschlichen Gehirns bestehen sie aus einer Vielzahl künstlicher Neuronen, die in Schichten organisiert und durch gewichtete Verbindungen miteinander verknüpft sind. Jedes Neuron empfängt Eingabesignale, verrechnet sie mit bestimmten Gewichten und erzeugt daraus eine Aktivierung, die an die nächste Schicht weitergegeben wird. So entsteht ein hierarchisches System der Informationsverarbeitung, das mit zunehmender Tiefe immer komplexere Merkmale aus den Eingangsdaten extrahiert.
Ein neuronales Netz lässt sich grob in drei Bereiche gliedern: die Eingabeschicht, die verborgenen (Hidden) Schichten und die Ausgabeschicht (Bild 1).
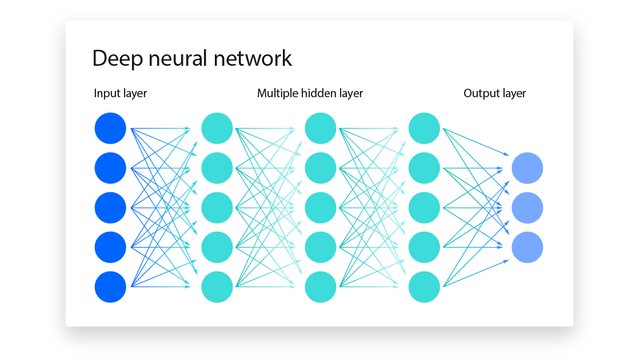
Die Eingabeschicht nimmt die Rohdaten auf, beispielsweise Pixelwerte eines Bildes oder numerische Merkmale eines Datensatzes. In den Hidden Layers findet die eigentliche Transformation statt – jede Schicht lernt auf Basis der Ausgaben der vorherigen Schicht neue Merkmale oder Muster. Die Ausgabeschicht schließlich liefert das Ergebnis, etwa eine Klassenzuordnung oder einen numerischen Vorhersagewert.
Mathematisch lässt sich der Prozess innerhalb eines Neurons wie folgt beschreiben:
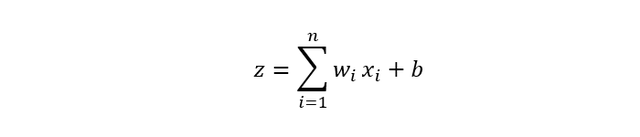
Dabei sind 𝑥𝑖 die Eingabewerte, wi die zugehörigen Gewichte und b ein Bias-Term, der als zusätzlicher Verschiebungsparameter fungiert. Das Zwischenergebnis z wird anschließend durch eine Aktivierungsfunktion f(z) transformiert, die bestimmt, wie stark das Neuron „feuert“. Die Ausgabe des Neurons ergibt sich somit zu: y = f(z)
Diese Aktivierungsfunktionen verleihen neuronalen Netzen ihre entscheidende Fähigkeit zur Nichtlinearität. Ohne sie könnten Netze nur lineare Zusammenhänge modellieren.
In der Praxis werden je nach Aufgabe verschiedene Funktionen eingesetzt, deren mathematische Definitionen und Eigenschaften sich wie in Bild 2 gezeigt tabellarisch gegenüberstellen lassen:

Aktivierungsfunktionen und ihre mathematischen Definitionen und Eigenschaften (Bild 2)
AutorBeim Training neuronaler Netze spielt die Fehlerrückführung – die sogenannte Backpropagation – eine zentrale Rolle. Zunächst wird ein Forward Pass ausgeführt, bei dem die Eingabedaten Schicht für Schicht verarbeitet werden und daraus eine Vorhersage erzeugt wird. Anschließend wird der Unterschied zwischen Vorhersage und Sollwert mit einer Loss-Funktion berechnet, etwa mit der mittleren quadratischen Abweichung (Mean Squared Error, MSE):
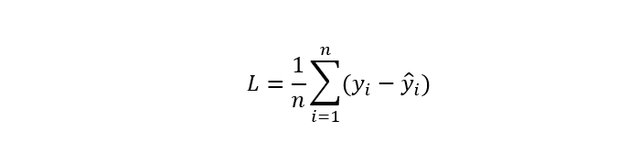
oder der Kreuzentropie (Cross Entropy) bei Klassifikationsaufgaben. Dieser Fehlerwert L wird rückwärts durch das Netz propagiert. Mithilfe der partiellen Ableitungen ծL/ծwi lässt sich bestimmen, wie stark jedes Gewicht zum Fehler beiträgt. Anschließend werden die Gewichte mit einem Optimierungsverfahren – typischerweise dem Gradient Descent – angepasst:
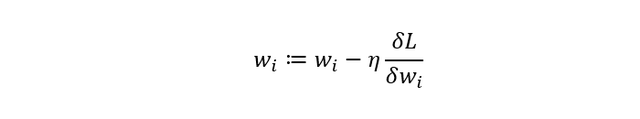
η ist die Lernrate, also die Schrittweite, mit der das Netz seine Gewichte korrigiert. Durch wiederholtes Anwenden dieses Prozesses über viele Trainingszyklen (Epochen) lernt das Netz, die Fehler zu minimieren und immer genauere Vorhersagen zu treffen.
Je nach Aufgabenstellung kommen unterschiedliche Netzwerkarchitekturen zum Einsatz. Multilayer Perceptrons (MLP) sind klassische Feedforward-Netze, die sich gut für strukturierte, tabellarische Daten eignen. Convolutional Neural Networks (CNNs) sind auf räumliche Daten wie Bilder spezialisiert und erkennen lokale Muster wie Kanten oder Formen. Für zeitliche oder sequenzielle Daten – etwa bei Sprache, Text oder Sensordaten – werden Rekurrente Neuronale Netze (RNNs) sowie deren erweiterte Varianten LSTM (Long short-term memory) und GRU (Gated Recurrent Unit), eingesetzt, die zeitliche Abhängigkeiten modellieren. In der modernen KI haben sich schließlich Transformer-Netzwerke durchgesetzt, die mithilfe sogenannter Attention-Mechanismen lange Kontextabhängigkeiten in Sequenzen erfassen und so die Grundlage für heutige Large Language Models bilden.
Die praktische Umsetzung neuronaler Netze erfolgt meist in Python mithilfe von Frameworks wie TensorFlow oder PyTorch.
TensorFlow versus PyTorch
TensorFlow und PyTorch verfolgen grundsätzlich verschiedene Ansätze:
- Rechenmodell: PyTorch verwendet standardmäßig einen dynamischen Rechengraphen (Eager Execution). Das bedeutet: Alle Operationen werden in Echtzeit ausgeführt und der Graph entsteht „on the fly“, was Debugging und flexible Modellanpassungen vereinfacht. TensorFlow (mit Keras) unterstützt zwar ebenfalls Eager Execution, arbeitet aber intern oft graphenbasiert: Hier wird das gesamte Modell vor dem Training als statischer Graph definiert, was effiziente Optimierungen etwa für verteiltes Rechnen oder die Produktion ermöglicht.
- Syntax und API: In PyTorch werden Modelle typischerweise als Klassen definiert und der Code ähnelt stark normalem Python. TensorFlow mit Keras bietet deklarative Schnittstellen wie Sequential-Modelle oder ein funktionales API. Beide Frameworks enthalten Schichten (zum Beispiel Dense, Conv2D) und Low-level-Interfaces. Keras ist dabei ein offizieller High-Level-Zugang zu TensorFlow, der besonders Einsteigern das Entwickeln von Modellen erleichtert.
- Ökosystem und Tools: TensorFlow bringt ein umfangreiches Ökosystem mit: TensorBoard zur Visualisierung von Training und Graphen, TensorFlow Lite für den mobilen Einsatz sowie Integrationen in Google-Cloud-Dienste. PyTorch hat spezialisierte Bibliotheken wie TorchVision (für Computer-Vision-Modelle und Datenaugmentation) und TorchText (für NLP), sowie die ONNX-Schnittstelle zum Export in andere Umgebungen. Beide Frameworks unterstützen GPU-Beschleunigung und verteiltes Training.
- Anwendungsfälle: PyTorch ist in Forschung und Lehre sehr verbreitet. Sein dynamisches Paradigma ermöglicht schnelles Prototyping und einfaches Debuggen. TensorFlow gilt als ausgereift und wird oft für produktionsreife, skalierbare Anwendungen eingesetzt (zum Beispiel bei großen Services oder Mobil-Deployments). Studien zeigen, dass beide Frameworks vergleichbare Genauigkeit liefern können, sodass die Wahl meist auf Basis von Präferenz und Projektanforderungen erfolgt.
Einfaches neuronales Netz mit TensorFlow/Keras
In diesem Tutorial bauen wir ein einfaches Bildklassifizierungs-Modell, das handgeschriebene Ziffern erkennt. Wir verwenden dazu den beliebten MNIST-Datensatz mit 60.000 Trainings- und 10.000 Testbildern von Ziffern (Bild 3).

Jedes Bild ist ein Graustufenbild der Größe 28×28 Pixel. Das Modell lernt, jedes Bild einer von zehn Klassen (den Ziffern 0 bis 9) zuzuordnen. In den folgenden Schritten zeigen wir, wie man die Daten lädt, ein Convolutional Neural Network (CNN) definiert, trainiert und auswertet. CNNs sind speziell dafür ausgelegt, Merkmale aus Bilddaten zu extrahieren – daher eignen sie sich gut für die Ziffernerkennung.
Datensatz laden und vorbereiten
- MNIST-Daten laden: TensorFlow/Keras bietet den MNIST-Datensatz direkt an. Mit mnist.load_data() erhalten wir (x_train, y_train) und (x_test, y_test) für Training (60k Bilder) und Test (10k Bilder).
- Daten skalieren: Die Pixelwerte liegen ursprünglich im Bereich 0 bis 255. Wir normieren sie auf den Bereich 0 bis 1 durch Division durch 255. Das verbessert das Training.
- Form anpassen: Convolutional Layers erwarten eine 3D-Eingabe (Höhe, Breite, Kanal). MNIST-Bilder sind Graustufen, also addieren wir eine Kanaldimension (1) hinzu, sodass die Form (28, 28, 1) beträgt.
- Label-Codierung: Die Ziffernlabels von 0 bis 9 kodieren wir als One-Hot-Vektoren (also einen 10-dimensionalen Vektor mit einer 1 an der Stelle der Ziffer).
Der Quellcode:
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
# 1. Daten laden
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
# 2. Pixelwerte normalisieren (0-255 -> 0-1)
x_train = x_train.astype('float32') / 255.0
x_test = x_test.astype('float32') / 255.0
# 3. Kanaldimension hinzufügen (28x28x1)
x_train = x_train[..., tf.newaxis] # Form: (60000, 28, 28, 1)
x_test = x_test[..., tf.newaxis] # Form: (10000, 28, 28, 1)
# 4. Labels in One-Hot codieren
num_classes = 10
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
print(f"Trainingsbilder: {x_train.shape[0]}, Testbilder: {x_test.shape[0]}")
print(f"Bildform: {x_train.shape[1:]} - Kanal: {x_train.shape[3]}")
Modell definieren
Unser Modell ist ein sogenanntes Convolutional Neural Network (CNN) (Bild 4) – das ist eine spezielle Form eines neuronalen Netzes, das besonders gut mit Bildern umgehen kann.
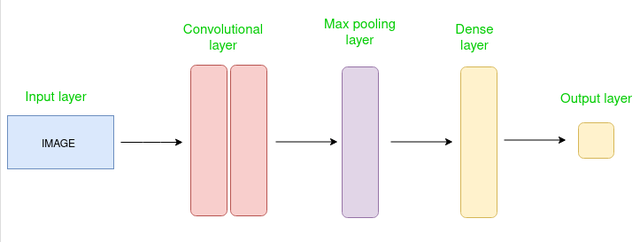
Statt jedes Pixel einzeln zu betrachten, sucht ein CNN nach kleinen, wichtigen Bildausschnitten – zum Beispiel Kanten, Rundungen oder andere Muster, die typisch für bestimmte Ziffern sind. Das Modell ist aus mehreren Schichten aufgebaut:
- Faltungsschicht (Conv2D) + Pooling: Die erste Schicht scannt das Bild mit kleinen Filtern (zum Beispiel 3×3 große Ausschnitte) und erkennt dabei einfache Formen. Danach sorgt eine Pooling-Schicht dafür, dass das Bild kleiner wird – dabei bleiben die wichtigsten Informationen erhalten, aber das Rechnen wird schneller.
- Noch eine Faltung + Pooling: Die nächste Runde schaut mit mehr Filtern (zum Beispiel 64) auf das Bild – diesmal erkennt das Netz schon etwas komplexere Muster wie Kreise oder ganze Ziffernformen.
- Abflachen + voll verbundene Schicht (Dense): Jetzt machen wir aus dem Bild einen langen Zahlenvektor (Flatten), den wir an eine „normale“ neuronale Schicht (Dense) weitergeben. Hier wird noch einmal alles miteinander kombiniert, bevor die Entscheidung fällt. Wir bauen hier auch eine kleine Schutzfunktion namens „Dropout“ ein, damit das Netz nicht zu einseitig lernt.
- Ausgabeschicht mit Softmax: Am Ende sagt das Netz: „Ich denke, dieses Bild ist zu X % eine 3, zu Y % eine 5 …“. Die Ziffer mit der höchsten Wahrscheinlichkeit ist dann die Vorhersage des Netzes.
model = keras.Sequential([ # Erster Convolutional-Block layers.Conv2D(32, (3,3), activation='relu', input_shape=(28,28,1)), layers.MaxPooling2D((2,2)), # Zweiter Convolutional-Block layers.Conv2D(64, (3,3), activation='relu'), layers.MaxPooling2D((2,2)), # Abflachen und Dense-Schichten layers.Flatten(), layers.Dense(128, activation='relu'), layers.Dropout(0.5), # dient der Regularisierung layers.Dense(num_classes, activation='softmax') ]) model.summary() # Optional: zeigt die Modell-Architektur an
Die model.summary()-Ausgabe könnte aussehen wie in Bild 5 gezeigt.
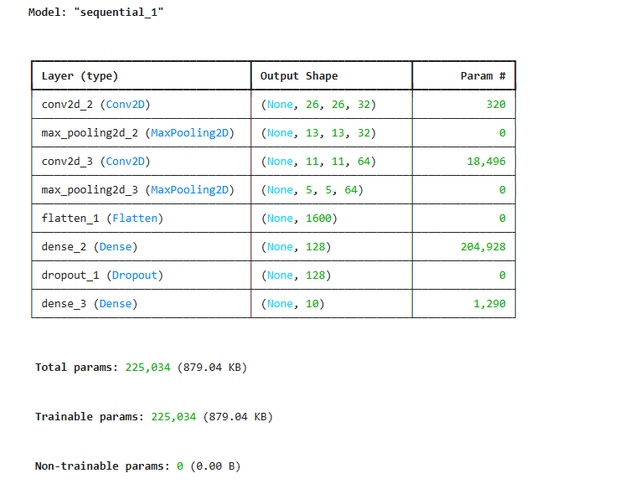
Modelldefinition – Ausgabe Jupyter-Notebook (Bild 5)
AutorWas sagen diese Werte:
- Conv2D (26×26×32): Das Eingabebild (28×28) wird durch 32 Filter (je 3×3) verarbeitet. Es entstehen 32 sogenannte Merkmalskarten mit je 26×26 Pixeln. Die 320 Parameter bestehen aus 32 Filtern à 9 Werte (3×3) plus je 1 Bias: 32×(3×3+1) =320.
- MaxPooling2D (13×13×32): Jedes Merkmalsbild wird halbiert – statt jedes Pixel zu behalten, wird pro 2×2-Bereich nur der größte Wert übernommen. Das reduziert die Rechenlast, ohne wichtige Informationen zu verlieren. Keine lernbaren Parameter.
- Conv2D (11×11×64): Jetzt analysiert das Netz die verdichteten Merkmalskarten mit 64 neuen Filtern. Es entstehen 64 neue Karten mit 11×11 Größe. Die 18.496 Parameter stammen aus 64×(3×3×32+1). Jeder neue Filter schaut auf alle 32 vorherigen Kanäle.
- MaxPooling2D (5×5×64): Wieder halbieren wir die Bildgröße – diesmal von 11×11 auf 5×5, mit 64 Kanälen. Keine lernbaren Parameter.
- Flatten (1600): Die dreidimensionalen Merkmalskarten werden in einen langen Vektor mit 1600 Zahlen umgewandelt. Keine Parameter – nur Umformung.
- Dense (128): Voll verbundene Schicht: Jeder der 1600 Eingabewerte ist mit 128 Neuronen verbunden. Das ergibt 1600×128+128=204.9281 trainierbare Gewichte (einschließlich Bias). Hier lernt das Netz abstrakte Zusammenhänge.
- Dropout: Beim Training werden zufällig Verbindungen „abgeschaltet“, um Überanpassung (Overfitting) zu vermeiden. Keine Parameter.
- Dense (10): Die Ausgabeschicht mit 10 Neuronen (eine für jede Ziffer 0–9). Die 1.290 Parameter stammen aus 128×10+10. Die Aktivierung (Softmax) liefert Wahrscheinlichkeiten für jede Klasse.
Das Modell hat insgesamt etwa 225.000 lernbare Parameter, die im Training aus Daten angepasst werden. Die Kombination aus Bildmerkmal-Erkennung (Conv2D), Verdichtung (Pooling) und Entscheidungslogik (Dense) ermöglicht sehr gute Ergebnisse bei der Ziffernerkennung.
Kompilieren und Training
Vor dem Training müssen wir das Modell kompilieren. Wir wählen typischerweise den Adam-Optimizer und als Verlustfunktion die Kategorielle Kreuzentropie (categorical_crossentropy), da wir ein Mehrklassen-Klassifikationsproblem haben. Zudem überwachen wir die Genauigkeit als Trainingsmetrik. Die Genauigkeit gibt an, wie oft die vorhergesagte Klasse mit dem richtigen Label übereinstimmt. In Keras sieht das so aus:
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
Jetzt trainieren wir das Modell. Wir verwenden zum Beispiel fünf Epochen und eine Batch-Größe von 64 (kann variieren). Keras zeigt nach jeder Epoche den Trainingsverlust und die Trainings-Genauigkeit (und gegebenenfalls Validierungs-Metriken) an.
history = model.fit(x_train, y_train, epochs=5, batch_size=64, validation_split=0.1) # optional: 10% der Trainingsdaten als Validation
In der Ausgabe sieht man beispielhaft Werte, wie sie in Bild 6 dargestellt sind.
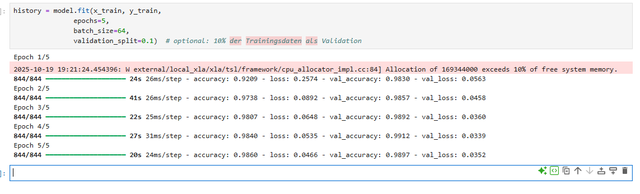
Modelltraining – Ausgabe Jupyter Notebook (Bild 6)
AutorDie accuracy-Werte liegen hier bereits nahe bei 95 bis 97 Prozent im Training.
Evaluation und Vorhersagen
Nach dem Training werten wir das Modell auf dem separaten Testdatensatz aus, um eine objektive Kennzahl zu erhalten. Dazu verwendet man zum Beispiel model.evaluate, was Verlust und Genauigkeit auf den Testdaten berechnet. Typischerweise erhält man hier eine Genauigkeit um 98 bis 99 Prozent, das heißt, dass von 100 Bildern etwa 98 bis 99 korrekt klassifiziert werden.
test_loss, test_acc = model.evaluate(x_test, y_test, verbose=0)
print(f"Testgenauigkeit: {test_acc*100:.2f}%")
Beispielausgabe: Testgenauigkeit: 98.02%
Um eine Vorhersage für einzelne Bilder zu erzeugen, ruft man model.predict auf. Da unsere letzte Schicht Softmax verwendet, liefert das Modell für jedes Bild eine Wahrscheinlichkeitsverteilung über die zehn Klassen. Die vorhergesagte Ziffer ist der Index mit der höchsten Wahrscheinlichkeit:
import numpy as np
predictions = model.predict(x_test[:5]) # Vorhersagen für die ersten 5 Testbilder
predicted_labels = np.argmax(predictions, axis=1)
true_labels = np.argmax(y_test[:5], axis=1)
print("Vorhergesagte Klassen:", predicted_labels)
print("Tatsächliche Klassen: ", true_labels)
Beispielausgabe: Vorhergesagte Klassen: [7 2 1 0 4]; tatsächliche Klassen: [7 2 1 0 4]
Hier stimmen die Vorhersagen mit den echten Labels überein.
Ergebnisinterpretation
Das Modell erreicht typischerweise eine sehr hohe Genauigkeit (um 98 bis 99 Prozent). Das bedeutet, dass fast alle Testbilder korrekt erkannt werden. Als Anfänger sollte man beachten: Eine hohe Genauigkeit ist zwar schön, aber das hier gewählte Beispiel ist vergleichsweise einfach (vorverarbeitete, zentrierte Ziffern). In komplexeren realen Anwendungen sind die Daten oft schwieriger.
- Genauigkeit (Accuracy): Anteil korrekt klassifizierter Bilder. Beispielsweise bedeutet 98 Prozent, dass 98 von 100 Bildern richtig erkannt wurden.
- Verlust (Loss): Maß für Fehler (hier Kreuzentropie). Ein niedriger Verlust geht mit hoher Genauigkeit einher, ist aber schwer direkt zu interpretieren.
Die Softmax-Ausgabe zeigt, mit welcher Wahrscheinlichkeit das Modell jede Ziffer sieht. Die höchste Wahrscheinlichkeit gibt die vorhergesagte Klasse an.
Fazit
Wir haben gezeigt, wie man mit TensorFlow/Keras ein einfaches CNN für Bilderkennung umsetzt. Der komplette Code ist lauffähig in einer Standard-Python-Umgebung mit installiertem TensorFlow.