Mykola Dobrochynskyy

15. Okt 2018

Lesedauer 13 Min.

Deep Learning

Künstliche Intelligenz, Teil 3

Ein künstliches neuronales Netz, kombiniert mit automatisiertem Lernen: Fertig ist das Werkzeug für die künstliche Intelligenz von heute.

Die revolutionären technologischen Erfindungen der Menschheit sind oft von den jeweiligen Vorbildern in Mutter Natur inspiriert. Die Tragflächen eines Flugzeugs folgen dem Vorbild des Vogelflügels, die Linse eines optischen Geräts arbeitet nach den gleichen physischen Prinzipien wie die Linse im Auge. Es gibt sogar die Wissenschaftsdisziplin Bionik (auch Biomimikry, Biomimetik oder Biomimese), welche sich mit der technischen Umsetzung und Anwendung von Konstruktionen, Verfahren und Entwicklungsprinzipien biologischer Systeme befasst. Schließlich hat Mutter Natur die Erfahrung von hundert Millionen Jahren. Dieser Auffassung waren auch die Neuro- und Computerwissenschaftler Mitte des letzten Jahrhunderts, als man sich von menschlicher Denkmaschine, dem Gehirn, zu den mathematischen Modellen der vernetzten Datenverarbeitung inspirieren ließ. Diese Modelle wurden Artificial Neural Networks (ANN) oder künstliche neuronale Netzwerke (KNN) genannt.In den ersten Teilen der Artikelserie wurde bereits eine Definition von künstlichen neuronalen Netzwerken und darauf basierenden Modellen des Deep Learning [1] gegeben.In diesem Teil vertiefen wir den Wissensstand und zeigen dann, wie KNNs lernen. Danach werden verschiedene KNN-Architekturen vorgestellt. Und zum Schluss folgt die süße Praxis nach der trockenen Theorie: Sie experimentieren mit dem Tensorflow-Playground [2].

Künstliche neuronale Netze

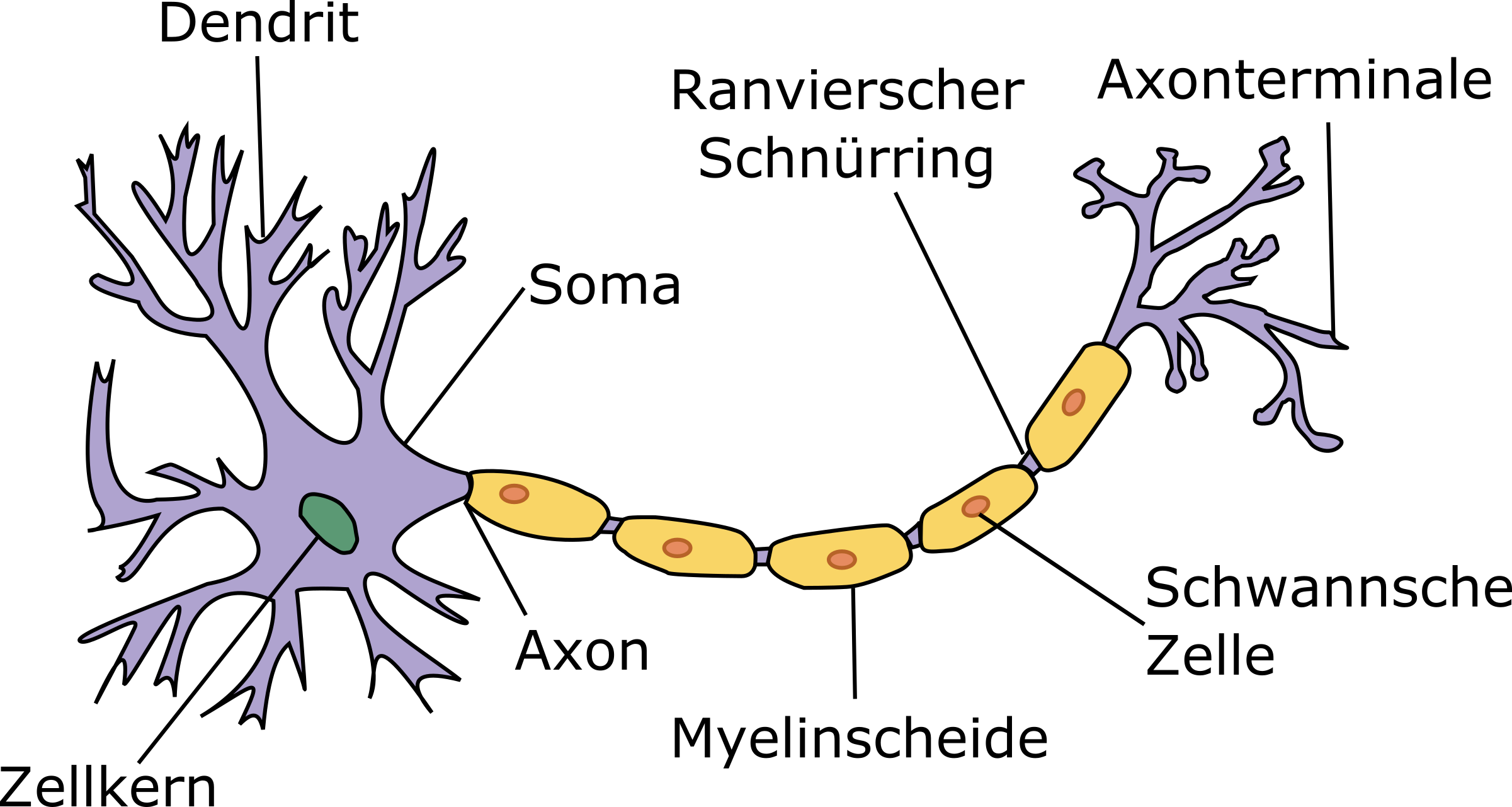
Ein künstliches neuronales Netzwerk stellt ein mathematisches Modell dar, das durch das Vorbild vernetzter biologischer Nervenzellen (Neuronen) inspiriert worden ist. Neuronen [3] sind spezielle Nervenzellen, die in der Gehirnrinde miteinander kommunizieren und so einen leistungsstarken biologischen Computer bilden. In einem menschlichen Gehirn befinden sich schätzungsweise 90 bis 200 Milliarden Neuronen mit jeweils sieben bis Zehntausenden Verbindungen. Laut letzten Studien [4] befinden sich in Gehirnrinde allein ca. 125 Trillionen neuronaler Verknüpfungen (Synapsen) [5]. Das entspricht ungefähr der Sternenanzahl von 1500 Galaxien. Ein einziges menschliches Gehirn enthält mehr Schalter als alle Computer, Router und Switches im Internet zusammengenommen!In Bild 1 ist eine Nervenzelle dargestellt. Sie besteht aus dem Zellkörper (oder Soma), vielen kurzen, verzweigten Zellvorsätzen – Dendriten – und einem langen schlauchartigen Zellvorsatz – dem Axon.

Das Axon, das manchmal bis zu einem Meter lang sein kann, dient als Signalausgang, der durch die vielen buschigen Axon-Terminale eine Verbindung (Synapsen) mit Neuron-Eingangspforten (Dendriten) bildet. Einzelne Synapsen können hemmend oder reizend auf die Signale von benachbarten Neuronen reagieren.Man unterscheidet bei der Aktivität eines Neurons zwischen dem Aktiv-Zustand – Senden eines Signals – und Inaktiv- oder Ruhezustand, wenn ein Neuron auf die Signale seiner benachbarten Neuronen lauscht. Der Übergang von einer Phase zur anderen wird durch von Dendriten aufgenommene äußere Reize angestoßen. Ein Neuron im Ruhezustand akkumuliert alle empfangenen Signale, bis eine bestimmte Aktivierungsschwelle erreicht ist.Inspiriert vom biologischen Neuron ist die Idee des künstlichen Neurons entstanden. Im Jahr 1943 haben die Mathematiker Warren McCulloch und Walter Pitts das Neuron als logisches Schwellenwertelement mit mehreren Eingängen und einem Ausgang in die Informatik eingeführt [2]. Es nimmt boolesche Werte entgegen und feuert ein Signal (wahr), wenn die Summe der Eingangssignale einen bestimmten Schwellenwert überschreitet. Nimmt man x_i als eines der Eingangssignale und w_i als dazu passendes Gewicht, so kann man die y-Ausgabe mathematisch wie in Bild 2 darstellen.

Dies wäre analog zum biologischen Neuron, wenn die jeweilige Nervenzelle nach der kritischen Änderung ihres Membranpotenzials ein Aktionspotenzial aussendet. McCulloch und Pitts haben gezeigt [2], dass mit einem oder einer geeigneten Kombination mehrerer Neuronen mit passenden Gewichten sich alle booleschen Funktionen implementieren lassen.Ein Nachteil dieses Modells war, dass es nicht automatisch lernen konnte. Jemand musste also manuell passende Gewichte und gegebenenfalls Neuronen-Kombinationen festlegen, um gewünschte Berechnungen zu ermöglichen. Dieser Nachteil konnte durch die nächste große Erfindung beseitigt werden: das Perceptron [3] (Wahrnehmer). Es wurde von Frank Rosenblatt im Jahre 1958 eingeführt [4]. Das Perzeptron-Modell lässt die Gewichte und den Schwellenwert durch verschiedene Varianten von Perzeptron-Regeln erlernen. Für einen binären Klassifikator (trennt Äpfel von Birnen) sieht die Lernregel wie in Bild 3 aus.

Dabei wäre ∆w_ij eine Gewichtsänderung für die Verbindung zwischen der Ausgabe des j-Neurons und Eingabe des i-Neurons, x_i, t_iund o_i sind hier jeweils gewünschte und tatsächliche Ausgaben des j-Neurons und (> 0) ein Lerngeschwindigkeits-Koeffizient, auch als Lernrate bekannt.Andere Varianten der Perzeptron-Lernregeln, wie zum Beispiel Maxover- oder Pocket-Algorithmus (siehe Details in [3]), sind für die komplexeren Fälle gedacht, wenn zum Beispiel der Trainingsdatensatz nicht linear separierbar ist (nicht mit einer Linie oder (Hyper-)Fläche geometrisch voneinander getrennt werden kann). Es gibt auch bekannte Probleme beim einlagigen Perzeptron-Modell, wie zum Beispiel das in [5] beschriebene XOR-Problem, welches aber durch sogenannte MLPs – mehrlagige Perzeptron-Modelle (engl. multi-layer perceptron) – gelöst werden kann.Ein mit dem Perzeptron-Modell konzipiertes künstliches Neuron (Bild 4) stellt auch heute die Grundlage moderner KNNs (künstlicher neuronaler Netzwerke) dar.

In Bild 4 kann man erkennen, dass ein künstliches Neuron sehr ähnlich zu seinem biologischen Prototyp aufgebaut ist, da es aus den folgenden Teilen besteht:

Eine oder mehrere eingehende Verbindungen x₁ bis x_n, welche numerische Ausgangssignale von anderen Neuronen empfangen. Dabei wird jeder Verbindung eine Gewichtung w_1j bis w_nj zugewiesen, die verwendet wird, um das jeweilige gesendete Signal zu verstärken beziehungsweise zu drosseln.
Eine (manchmal mehrere) Ausgangsverbindung, die das Ergebnis-Signal o_jzu den anderen Neuronen überträgt.
Eine Aktivierungsfunktion , die den numerischen Wert des Ergebnissignals bestimmt, das das Neuron aussendet. Vorher werden alle ausgewogenen Eingangssignale von anderen Neuronen als Netzeingabe net_i aufsummiert und mit eigener Aktivierungsschwelle _i als Argumente der Aktivierungsfunktion verwendet.

Die Aktivierungsfunktionen [6] (auch als Übertragungsfunktionen bekannt) haben gewöhnlich einen dynamischen Ausgabebereich zwischen -1 und 1 oder zwischen 0 und 1, wobei bei einigen die Ausgabegrenzen breiter sein beziehungsweise ins Unendliche gehen können. Viele Aktivierungsfunktionen unterscheiden sich in ihrer Komplexität und Ausgabeart. In der Tabelle in Bild 5 kann man häufig benutzte Aktivierungsfunktionen wie Schritt-, Linear-, Sigmoid-, Tangens- und ReLU-Funktion und in [6] eine ziemlich umfangreiche Liste verschiedener anderer Aktivierungsfunktionen nachschlagen.

Gradient (G)

Der Gradient [24] ist ein mathematischer Operator, genauer ein Differentialoperator, der auf ein Skalarfeld angewandt werden kann und in diesem Fall ein Gradientenfeld genanntes Vektorfeld liefert. Der Gradient steht dabei senkrecht auf der Niveaufläche (Niveaumenge) des Skalar-Feldes in einem Punkt P und der Betrag des Gradienten gibt die Änderungsrate des Skalarfeldes im Punkt P an.

Außer der Art eines Problems, das ein neuronales Netzwerk lösen soll, wie zum Beispiel die Klassifikation oder die Regression [7], spielt auch die Auswahl geeigneter Parameter eines Deep Learning Models eine wichtige Rolle, um ein qualitatives und performantes Training durchführen zu können. Diese Themen werden intensiv erforscht [6] und es werden gute Ergebnisse in Bezug auf die Ausgabequalität bestätigt, wenn die Trainingsphase ordnungsgemäß durchgeführt worden ist. Für eine gut gelungene Trainingsphase eines Deep Learning Models (mehrschichtiges neuronales Netz) spielen folgende Parameter eine Schlüsselrolle:

Aktivierungsfunktion
Eingangsdaten- und Gewichte-Initialisierung
Lernrate
Regularisierungsart und -rate
Splitting (Aufteilung von Training- und Test-Datensätzen)
Größe des Testdatenpakets (engl. batch-size)
Anzahl der Testläufe (engl. epoch)

Bei der Auswahl einer Aktivierungsfunktion gibt es keine Faustregel. Alles hängt von den Netzeingabedaten ab und auch davon, in welcher Form diese Daten nach Aktivierungsfunktionsaufruf umgewandelt werden sollen. Wenn Sie eine bestimmte Aktivierungsfunktion auswählen möchten, muss man relevante Funktionsgraphen analysieren, um zu sehen, wie sich das Ergebnis in Bezug auf die angegebenen Werte ändert.Ein interessanter Fall wäre die Softmax-Aktivierungsfunktion (Bild 5 und [6][9]), welche anstatt eines einzigen Netzausgabewertes (Netzausgabevektor) ein Dutzend davon nimmt und entsprechend den Wahrscheinlichkeitswertanteil als Ergebnis für jedes Element des Netzausgabevektors liefert, wobei die Summe aller Wahrscheinlichkeitswerte logischerweise immer eins ist (Bild 6).Als Beispiel sei auf einen anderen Artikel des Autors zur Emotionserkennung mit Microsoft Cognitive Services [10][11] verwiesen. Listing 1 zeigt das Ergebnis des Emotionsdienstes auf das Bild eines überraschten Jungen. Der Emotionswert surprise beträgt hier 0,9273863 oder in Prozent ausgedrückt ca. 93 Prozent. Alle anderen Emotionen sind ziemlich marginal und machen zusammen mit dem Emotionswert surprise eine Eins aus.

Listing 1: KI-Dienstantwort mit Softmax-Aktivierungsfunktion

[ &lt;br/&gt;  { &lt;br/&gt;    &lt;span class="hljs-attr"&gt;"faceRectangle"&lt;/span&gt;: { &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"top"&lt;/span&gt;: &lt;span class="hljs-number"&gt;141&lt;/span&gt;, &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"left"&lt;/span&gt;: &lt;span class="hljs-number"&gt;130&lt;/span&gt;, &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"width"&lt;/span&gt;: &lt;span class="hljs-number"&gt;162&lt;/span&gt;, &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"height"&lt;/span&gt;: &lt;span class="hljs-number"&gt;162&lt;/span&gt; &lt;br/&gt;    }, &lt;br/&gt;    &lt;span class="hljs-attr"&gt;"scores"&lt;/span&gt;: { &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"anger"&lt;/span&gt;: &lt;span class="hljs-number"&gt;9.29041E-06&lt;/span&gt;, &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"contempt"&lt;/span&gt;: &lt;span class="hljs-number"&gt;0.000118981574&lt;/span&gt;, &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"disgust"&lt;/span&gt;: &lt;span class="hljs-number"&gt;3.15619363E-05&lt;/span&gt;, &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"fear"&lt;/span&gt;: &lt;span class="hljs-number"&gt;0.000589638&lt;/span&gt;, &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"happiness"&lt;/span&gt;: &lt;span class="hljs-number"&gt;0.06630674&lt;/span&gt;, &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"neutral"&lt;/span&gt;: &lt;span class="hljs-number"&gt;0.00555004273&lt;/span&gt;, &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"sadness"&lt;/span&gt;: &lt;span class="hljs-number"&gt;7.44669524E-06&lt;/span&gt;, &lt;br/&gt;      &lt;span class="hljs-attr"&gt;"surprise"&lt;/span&gt;: &lt;span class="hljs-number"&gt;0.9273863&lt;/span&gt; &lt;br/&gt;    } &lt;br/&gt;  } &lt;br/&gt;]

Wie lernt ein KNN?

Wie in [12] bereits erwähnt wurde, findet der Lernprozess eines neuronalen Netzwerks als eine sich wiederholende Gewichteoptimierung statt, indem man die Netzwerkausgabe mit den erwarteten Werten vergleicht. Das stellt also einen Fall des überwachten Lernens [13] dar. Die Gewichteoptimierung wird typischerweise mit dem sogenannten Backpropagation-Algorithmus (oder Backprop) durchgeführt [12][14], indem man versucht, eine spezielle Zielfunktion [15] (auch Verlustfunktion) zu minimieren. Eine Zielfunktion zeigt an, inwieweit sich die tatsächlichen Ausgabewerte von den erwarteten Werten unterscheiden. Es gibt folgende Hauptschritte bei einem Backprop-Algorithmus:

Initialisierung: Das Netzwerk wird mit zufälligen Werten initialisiert.
Vorwärtsdurchlauf (forward pass): Läuft für alle Netzwerkschichten in die Richtung von der Eingabe- zur Ausgabeschicht. Dabei wird der Netzwerkfehler berechnet – eine Differenz zwischen der gewünschten und der tatsächlichen Ausgabe.
Rückwärtsdurchlauf (backward pass): Läuft für alle Netzwerkschichten in die entgegengesetzte Richtung – von Ausgabe- zu Eingabeschicht. Dabei wird der Netzwerkfehler der äußersten Schicht minimiert, indem man das Gewicht von Neuronen der nachstehenden Vorgängerschicht minimiert. Diesen Vorgang nennt man Optimierungsschritt der Backpropagation.
Iterationen (eng. epochs): Vorwärts- und Rückwärtsdurchläufe werden zyklisch über den Datensatz durchgeführt, bis der Fehler in dem Validierungssatz zuzunehmen beginnt. Dies kann auf eine Überanpassung [16] (Overfitting) deuten. Das heißt, die Phase, in der das Netzwerk zu spezifisch wird und anfängt, die Trainingsdaten auf Kosten der Generalisierbarkeit zu interpolieren.

Um die Gewichteoptimierung zu organisieren, braucht man einen Algorithmus, der die Gewichtungen von künstlichen Neuronen effizient optimieren kann. Dafür kann ganz gut eine numerische iterative Technik namens Gradientenverfahren oder besser bekannt als Gradient Descent (GD) [17] verwendet werden. Ein solcher GD-Algorithmus läuft wie folgt:

Initialisierung: Das Modell wird mit zufälligen Gewichten (w) initialisiert.
Gradient (_wJ) berechnen: Ein Gradient (siehe Kasten Gradient) wird mit der Berücksichtigung jedes relevanten Gewichts w berechnet.
Gradientenabstieg: Gewichte (w) werden so angepasst, dass Gradient _wJ und Verlustfunktion J(w) sinken (Bild 7).

Verlustfunktion minimieren: Gradientenabstieg schrittweise wiederholen, bis Gradient minimalen Wert erreicht _wJ = 0 (siehe Bild 7). Bei nichtkonvexen Zielfunktionen (diese können mehrere Gradient-Minimumpunkte haben) muss man versuchen, ein globales Minimum zu erreichen und nicht bei lokalen Tiefpunkten (siehe Bild 8) stecken zu bleiben.

Ziemlich häufig hat man es mit (sehr) großen Trainingsdatensätzen zu tun. Wenn man auf die gesamte Datenmenge einen GD-Algorithmus anwenden würde, würde die Gewichteoptimierung sehr lange dauern, was die Effizienz eines KNNs stark beeinträchtigten und zu unnötigen Latenzeffekten und erhöhten Rechenleistungsansprüchen führen könnte. In diesem Fall wendet man statt Gradient Descent einen Stochastic-Gradient-Descent-Algorithmus (SGD) an (siehe [18] und Bild 9).

Der Begriff stochastisch kommt daher, dass das Gradientenverfahren nicht auf dem gesamten Trainingsdatensatz, sondern lediglich auf einzelnen zufälligen Punkten basiert – zum Beispiel pickt man fünf bis zehn Prozent der Datenpunkte des gesamten Datensatzes zufällig heraus, mit guten Chancen, gegebenenfalls lokale Gradienten-Zero-Punkte zu vermeiden und ein globales Gradientenminimum zu finden. Aufgrund der stochastischen Natur des SGD-Verfahrens verläuft der Weg zum globalen Kostenminimum nicht direkt wie beim GD-Algorithmus, sondern kann im Zickzack verlaufen (siehe Bild 9).

Paketgröße (eng. batch size)

Die Paketgröße definiert die Anzahl der Trainingsdatenpunkte in jedem Paket des Trainingsdatensatzes. Das Trainingspaket soll kompakt sein und dennoch groß genug, um eine möglichst genaue Annährung an den Gradienten des gesamten Trainingsdatensatzes zu garantieren. Gleichzeit muss ein Trainingspaket relativ rauschig sein, um lokale Gradienten-Minima zu vermeiden.

Deep Learning ausprobieren

Im zweiten Teil der Artikelserie wurde bereits eine Definition von Deep-Learning-(DL) KI-Modellen vorgestellt (siehe [12] und Kasten Deep Learning). Hier sollen ein paar Experimente ein Gefühl dafür geben, wie der Lernprozess eines Deep-Learning-Netzwerks aussieht.Um mit Deep-Learning-Modellen im Webbrowser ohne zusätzliche Softwareinstallation experimentieren zu können, gibt es zwei hervorragende Open-Source-Apps: den Tensorflow Playground [19][20] und die ConvNetJS-Bibliothek [21][22][23].Tensorflow Playground ist von zwei Entwicklern aus dem Google-Brain-Team entwickelt worden: Shan Carter und Daniel Smilkov. Die Web-App basiert wiederum auf der 2D-Klassifikationsdemo, einer Beispiel-JavaScript-Lösung [22] zur ConvNetJS-Bibliothek [21], die zu PhD-Studienzeiten an der Stanford-Uni von Teslas AI-Director Andrej Karpathy entwickelt worden ist.Fünf KI-Experimente sollen zeigen, wie das funktioniert:

Zwei Regressionsexperimente mit dem Tensorflow Playground und der ConvNet-Bild-Regressionsdemo [23] (Experimente Nummer eins und fünf).
Drei Klassifikationsexperimente mit Tensorflow Playground (Experimente zwei bis vier).

In der Tensorflow-Playground-Web-App kann man unterschiedliche Ein-/Ausgabe-Parameter einstellen/analysieren – unter anderem auch diejenigen, die im zweiten Kapitel bereits erwähnt wurden:

Problemtyp: Regression oder Klassifikation
Netzwerktopologie: Anzahl von verdeckten Schichten (eine bis sechs verdeckte Schichten) und Neuronenanzahl in jeder Schicht (ein bis acht Neuronen pro Schicht)
Aktivierungsfunktion
Lernrate
Regularisierungsart und -rate
Splitting (Aufteilung von Trainings- und Testdatensätzen)
Größe des Testdatenpakets (batch size)
Anzahl der Testläufe (epoch)
Trainingsverlustfunktion
Testverlustfunktion

Die ersten sieben der oben beschriebenen Parameter sind die Eingabe- und die letzten drei die Ausgabeparameter. Bei den ersten vier Experimenten mit Tensorflow-Playground werden Sie an den ersten vier Parametern drehen und die Auswirkungen solcher Anpassungen beobachten.

Iterationen (eng. epochs)

Eine Iteration (eng. epoch) bedeutet einen vollen Trainingsdurchlauf (Vorwärts- und Rückwärtsläufe) über den gesamten Trainingsdatensatz.

Beim ersten Experiment konnte ein Modell mit drei verdeckten Schichten mit je sechs, vier und zwei Neuronen für eine Regressionsaufgabe mit Lernrate 0,1 ganz schnell mit hervorragenden Testergebnissen trainiert werden (Bild 11). Das ist auch verständlich, da auf dem Datenausgabebild zu sehen ist, dass die zwei Datenmengen linear verteilt sind.

Im zweiten Versuch macht man demselben künstlichen neuronalen Netzwerk das Leben schwerer, indem man spiralförmige Daten zu klassifizieren versucht (Bild 12). Diese sind nicht linear separierbar.

Und tatsächlich ist zu sehen, dass man hier im Vergleich zum ersten Experiment ungefähr viermal so viele Durchläufe braucht, um auf vernünftige Werte bei der Verlustfunktion zu kommen.Außerdem verläuft die Zielfunktion (Verlustfunktion) ziemlich unruhig mit vielen Ausrutschern, was auf Overfitting (Überanpassung) [18] hindeutet. Man kann diese Störung minimieren, indem man Lerniterationen in kleineren Schritten durchführt.Und das ist genau, was beim dritten Experiment passiert ist (Bild 13): Die Lernrate ist um den Faktor zehn reduziert, was die Überanpassung (fast) beseitigt hat. Dafür hat es länger gedauert und zu schlechteren Verlustwerten bei den Testdaten geführt.

Das vierte Experiment geht aufs Ganze: Man modelliert ein KNN mit sechs verdeckten Schichten mit je acht Neuronen und nimmt ReLU als Aktivierungsfunktion (Bild 14). ReLU steht für Rectified Linear Unit. Sie hat den Ruf, eine effizientere und schnellere Aktivierungsfunktion zu sein, was sich auch bei Experiment vier bestätigt – bei deutlich größerem Modell mit 48 Neuronen hat man zweimal so wenige Iterationen (epochs) gebraucht wie zum Beispiel beim zweiten Experiment mit zwölf Neuronen.

Deep Learning (DL)

Deep Learning ist ein Optimierungsverfahren von künstlichen neuronalen Netzwerken (siehe [25] und <span class="text-bildnachweis">Bild 10</span>) mit umfangreicher inneren Struktur, die durch mehrere versteckte Zwischenlagen (engl. hidden layers) zwischen Ein- und Ausgabeschichten aufgebaut wird.

Beim fünften Experiment lässt man das KNN ein eigenes Bild von einem originalen Bild nachmalen (Bild 15). Allerdings behandelt man „unter der Haube“ die Pixel eines Bildes als ein Lernproblem – man nehme die (x,y)-Position auf dem Bildgitter und lernt, die Farbe an diesem Punkt durch die Regression zu RGB-Farbcodierung vorherzusagen.

All diese Experimente sind in der Tabelle in Bild 16 zusammengefasst.

Fazit

Mathematische Modelle wie Perzeptron, künstliche neuronale Netzwerke und darauf basierende Deep-Learning-Modelle mit mehreren Schichten miteinander verbundener künstlicher Neuronen sind von ihren biologischen Vorbildern inspiriert.Wie im theoretischen Teil behauptet und beim Experimentieren im letzten Kapitel gesehen, hängen die Qualität und die Trainings-/Testergebnisse eines Modells sehr von vielen Parametern ab wie initiale Daten, Gewichtungen, Aktivierungsfunktionen, Netztopologie, Lerngeschwindigkeit und so weiter.Maschinelles Lernen ist also keine Mathematik oder Physik, wo man mit einem Stift und einem Stück Papier große Fortschritte machen kann.Es ist eine Ingenieurswissenschaft. Viel Spaß beim Ausprobieren und viel Glück bei der Vorhersage!

Fussnoten

Deep Learning, http://www.dotnetpro.de/SL1811DeepLearning1
A logical calculus of the ideas immanent in nervous activity. WS McCulloch, W Pitts. Bull Math. Biophys., 5, 115–133, 1943, http://www.dotnetpro.de/SL1811DeepLearning2
Perzeptron, http://www.dotnetpro.de/SL1811DeepLearning3
The Perceptron – a probabilistic model for information storage and organization in the brain. F. Rosenblatt. Psychological Review 65, 1958, http://www.dotnetpro.de/SL1811DeepLearning4
M. L. Minsky und S. A. Papert, Perceptrons. 2nd Edition, MIT-Press, 1988, ISBN 0-262-63111-3, http://www.dotnetpro.de/SL1811DeepLearning5
Activation Function, http://www.dotnetpro.de/SL1811DeepLearning6
Mykola Dobrochynskyy, Vom Machine Learning zum Deep Learning, dotnetpro 09/18, S. 84ff, http://www.dotnetpro.de/A1809DeepLearning
Ian Goodfellow, Yoshua Bengio, Aaron Courville. Deep Learning (Adaptive Computation and Machine Learning). MIT Press, 2016, http://www.dotnetpro.de/SL1811DeepLearning7
Softmax function, http://www.dotnetpro.de/SL1811DeepLearning8
Mykola Dobrochynskyy, Gesicht, Emotionen, Videos, dotnetpro 12/17, S. 72ff, http://www.dotnetpro.de/A1712KI
Microsoft Azure Cognitive Services. Emotionserkennung, http://www.dotnetpro.de/SL1811DeepLearning9
Mykola Dobrochynskyy, In die Tiefe von Deep Learning, dotnetpro 10/18, S. 79ff, http://www.dotnetpro.de/A1810DeepLearning
Überwachtes Lernen, http://www.dotnetpro.de/SL1811DeepLearning10
Backpropagation, http://www.dotnetpro.de/SL1811DeepLearning11
Verlustfunktion, http://www.dotnetpro.de/SL1811DeepLearning12
Überanpassung, http://www.dotnetpro.de/SL1811DeepLearning13
Gradient Descent, http://www.dotnetpro.de/SL1811DeepLearning14
Stochastic gradient descent, http://www.dotnetpro.de/SL1811DeepLearning15
An open source machine learning frameworkTensorflow Playground. Web-App, http://www.dotnetpro.de/SL1811DeepLearning16
Tensorflow Playground. GitHub Repository, http://www.dotnetpro.de/SL1811DeepLearning17
A. Karpathy. ConvNetJS Library, http://www.dotnetpro.de/SL1811DeepLearning18
A. Karpathy. Demo – 2D Classification mit ConvNetJS, http://www.dotnetpro.de/SL1811DeepLearning19
A. Karpathy. Demo – Bild-Regression mit ConvNetJS, http://www.dotnetpro.de/SL1811DeepLearning20
Gradient (Mathematik), http://www.dotnetpro.de/SL1811DeepLearning21
Künstliches neuronales Netz, http://www.dotnetpro.de/SL1811DeepLearning22

Neueste Beiträge

Data & Analytics

DWX hakt nach: Wie stellt man Daten besonders lesbar dar?

Dass das Design von Websites maßgeblich für die Lesbarkeit der Inhalte verantwortlich ist, ist klar. Das gleiche gilt aber auch für die Aufbereitung von Daten für Berichte. Worauf besonders zu achten ist, erklären Dr. Ina Humpert und Dr. Julia Norget.

3 Minuten

DWX Redaktion

27. Jun 2025

Mehr erfahren

UI/UX

DWX hakt nach: Wie gestaltet man intuitive User Experiences?

DWX hakt nach: Wie gestaltet man intuitive User Experiences? Intuitive Bedienbarkeit klingt gut – doch wie gelingt sie in der Praxis? UX-Expertin Vicky Pirker verrät auf der Developer Week, worauf es wirklich ankommt. Hier gibt sie vorab einen Einblick in ihre Session.

4 Minuten

DWX Redaktion

27. Jun 2025

Mehr erfahren

Artificial Intelligence

„Sieh die KI als Juniorentwickler“

CTO Christian Weyer fühlt sich jung wie schon lange nicht mehr. Woran das liegt und warum er keine Angst um seinen Job hat, erzählt er im dotnetpro-Interview.

15 Minuten

Christian Weyer

27. Jun 2025

Mehr erfahren

Miscellaneous

Das könnte Dich auch interessieren

UI/UX

UIs für Linux - Bedienoberflächen entwickeln mithilfe von C#, .NET und Avalonia

Es gibt viele UI-Frameworks für .NET, doch nur sehr wenige davon unterstützen Linux. Avalonia schafft als etabliertes Open-Source-Projekt Abhilfe.

16 Minuten

Roland König

16. Jun 2025

Project Management & Methodologies

Mythos Motivation - Teamentwicklung

Entwickler bringen Arbeitsfreude und Engagement meist schon von Haus aus mit. Diesen inneren Antrieb zu erhalten sollte für Führungskräfte im Fokus stehen.

13 Minuten

Uwe Vigenschow

19. Jan 2017

Artificial Intelligence

Evolutionäres Prototyping von Business-Apps - Low Code/No Code und KI mit Power Apps

Microsoft baut Power Apps zunehmend mit Features aus, um die Low-Code-/No-Code-Welt mit der KI und der professionellen Programmierung zu verbinden.

19 Minuten

Dr. Manfred Simon

16. Jun 2025