15. Aug 2022
Lesedauer 13 Min.
Clevere Lösungen
Methoden des Operation Research, Teil 2
Die Entwicklung eines Optimierungsalgorithmus ist schwierig. Die Google OR-Tools zeigen hierbei großes Potenzial.
Autor
Über die Anwendungen und die Lösungsansätze (Algorithmen) von Optimierungsproblemen hat der erste Teil dieser Serie ausführlich berichtet [1]. Die Fragen kommen aus dem Bereich Transport (kürzeste Wege), Personalplanung (Schichtpläne bei Beachtung von allerlei Nebenbedingungen), der Produktionsplanung (Zuteilung von Maschinenkapazitäten) und so weiter. Um diese Probleme zu lösen, gibt es eine Reihe von etablierten Algorithmen und Heuristiken, zum Beispiel Verfahren der linearen Programmierung oder Routing-Algorithmen, die dafür eingesetzt werden können und sich auch bewährt haben.In der Programmierpraxis ist das Verständnis und der grundsätzliche Lösungsansatz das eine; der andere Aspekt ist das Entwickeln des konkreten Algorithmus. Das ist nicht einfach, doch mithilfe von Bibliotheken lässt sich der Weg erheblich abkürzen. Dazu gehören auch die Google OR-Tools, die in diesem Artikel vorgestellt werden [2].
Installation
Die Bibliothek selbst ist in C++ programmiert. Es liegen jedoch Wrapper (SDK) für die Anwendung in den Programmiersprachen Python, Java und für die .NET-Plattform (C#) vor. Von Interesse ist hier logischerweise letztere Variante. Entwickler haben die Wahl zwischen den kompilierten Bibliotheken und den Quellen, um die Bibliotheken selbst zu kompilieren. Es werden Binärdateien und Quellen für die Betriebssysteme Windows, macOS und Linux angeboten. Üblicherweise wird man die kompilierten Versionen der Bibliotheken nutzen.Wer die Google OR-Tools an eigene Probleme anpassen will oder diese tief in eigene Verfahren einbinden möchte, der benötigt die Pakete mit dem Quellcode. In diesem Artikel geht es um die Installation der binären Bibliotheken für Windows. Die Systemvoraussetzungen lauten:- Windows 10, 64-bit (x86_64)
- Microsoft Visual Studio 2019 oder 2022
- Microsoft Visual C++ Redistributable, Version x64
- .NET Core 2.1 SDK Version 2.1.302 oder höher
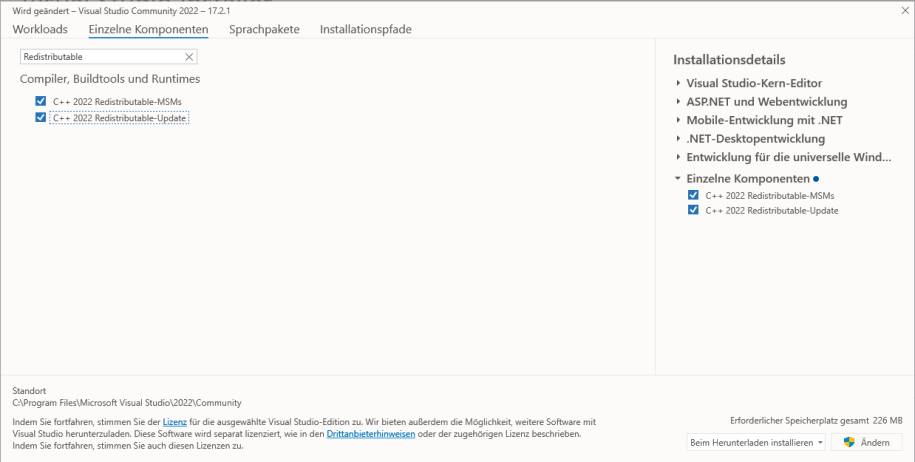
Die Installationder Redistributable-Bibliotheken über Visual Studio(Bild 1)
Autor
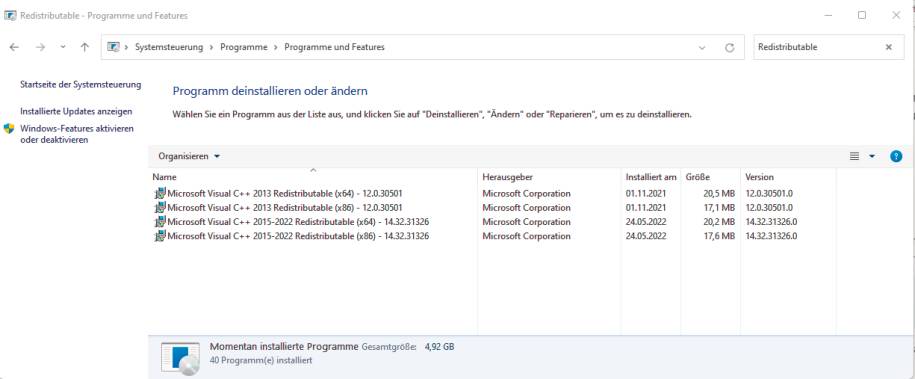
Prüfungder Voraussetzungen in der Systemsteuerung(Bild 2)
Autor
Die eigentliche Bibliothek laden Sie dann von der Webseite des Projekts als ZIP-Archiv. Um die Integrität des Downloads zu testen, entpacken Sie das Archiv, benennen es mithilfe eines handhabbaren Namens um (naheliegend wäre „ORTools“) und rufen die PowerShell-Konsole für das Verzeichnis auf. Dort geben Sie folgenden Befehl ein:
tools\<span class="hljs-built_in">make</span> test_dotnet
Dies stößt einen Testlauf für einige Beispiele der Bibliothek an. Die Ergebnisse werden in der Konsole angezeigt und sollten keinen Fehler ausweisen (Bild 3). Danach können Sie mit dem ersten Beispielen starten.
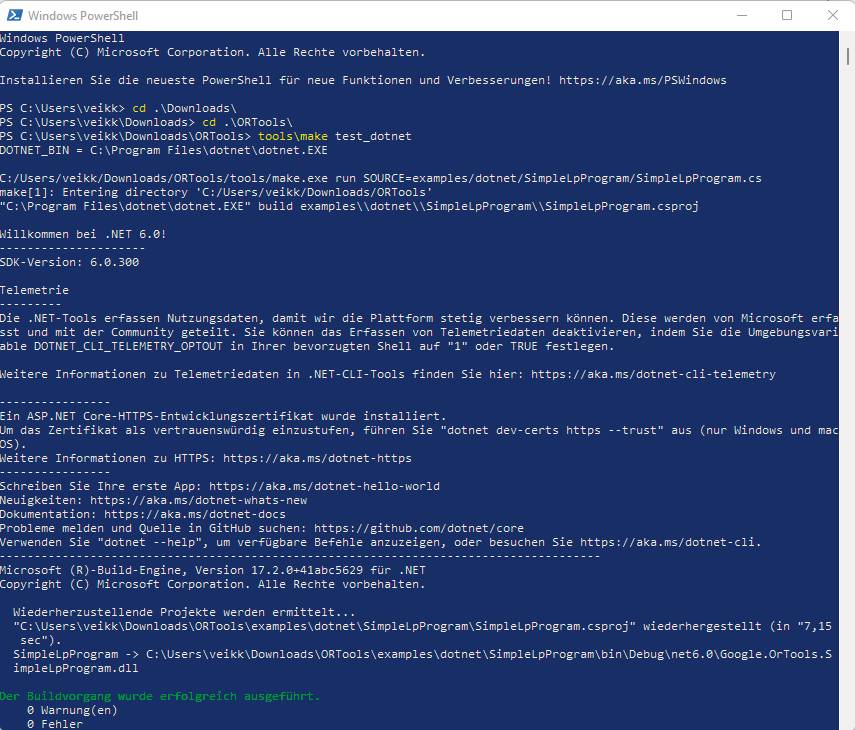
Der Testder Bibliothek in der PowerShell(Bild 3)
Autor
Um die Google OR-Tools zu verwenden, können Sie diese in eigenen Projekten auf herkömmliche Weise über den öffentlichen NuGet-Paketmanager einrichten. Suchen Sie – beispielsweise in einer neuen Konsolen- oder Windows-Forms-Anwendung – nach der entsprechenden Bibliothek mit der Bezeichnung Google.OrTools und installieren Sie diese im Projekt. Mit ihr haben Sie Zugriff auf die entsprechenden Methoden und Klassen.
Erste Gehversuche
Die Beispiele, die dem gerade heruntergeladenen ZIP-Archiv beigefügt sind, eignen sich sehr gut für den Einstieg. Im entpackten Archiv sind sie im Unterordner examples zu finden, sortiert nach den Programmiersprachen C++, Java und .NET (C#).Die Beispiele decken eine Reihe von typischen Problemfällen ab, die sich mit den Google OR-Tools lösen lassen, und können eine gute Ausgangsbasis sein, um die Algorithmen der Google OR-Tools in eigenen Programmen und für ähnliche Optimierungsprobleme anzuwenden.Um ein Beispiel zu testen, wählen Sie Traveling Salesperson Problem (TSP) [3], auf Deutsch das „Problem des Handlungsreisenden“. Google liefert zum TSP gleich mehrere Beispiele, die von der Grundversion ausgehend zunehmend umfassendere Restriktionen und Konkretisierungen ergänzen. Nun testen Sie das Grundbeispiel – zunächst auf Ebene der Kommandozeile: Gehen Sie zur Eingabeaufforderung und arbeiten Sie sich bis zum Ordner …\examples\dotnet\Tsp\bin\Debug\net6.0 vor. Er enthält die kompilierte Beispielanwendung und unter anderem auch eine ausführbare EXE-Datei. Rufen Sie diese auf. Das Programm wird ausgeführt und gibt das Ergebnis der Optimierung direkt auf der Konsole aus (Bild 4).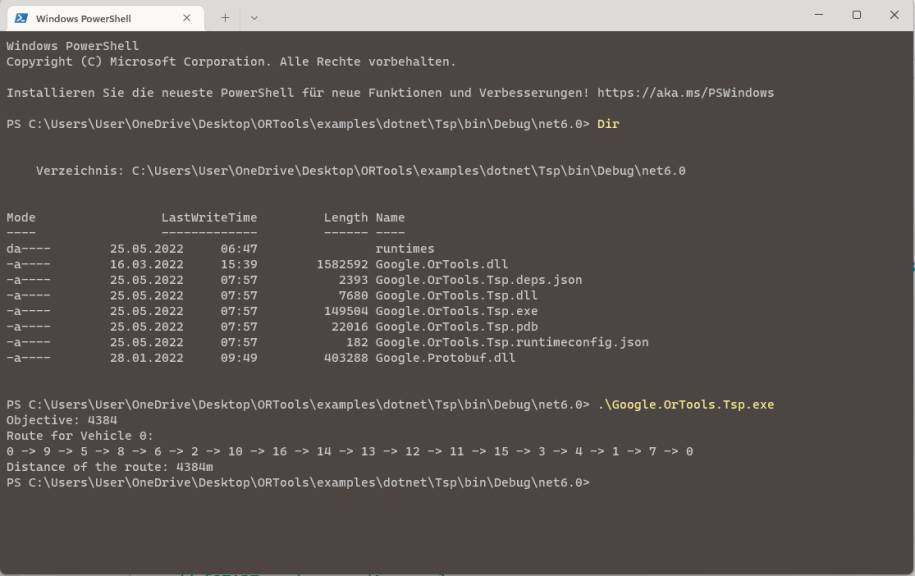
Die Ausführungdes TSP-Beispielprogramms und Ergebnisanzeige(Bild 4)
Autor
Das Problem des Handlungsreisenden
Die Aufgabe besteht darin, eine Reihenfolge für den Besuch mehrerer Orte eines Handlungsreisenden so zu wählen, dass kein Ort außer dem ersten Standort (Depot, Lager) mehr als einmal besucht wird. Die gesamte zurückgelegte Strecke des Handlungsreisenden soll dabei möglichst kurz und die letzte Station gleich der ersten Station sein (Bild 5).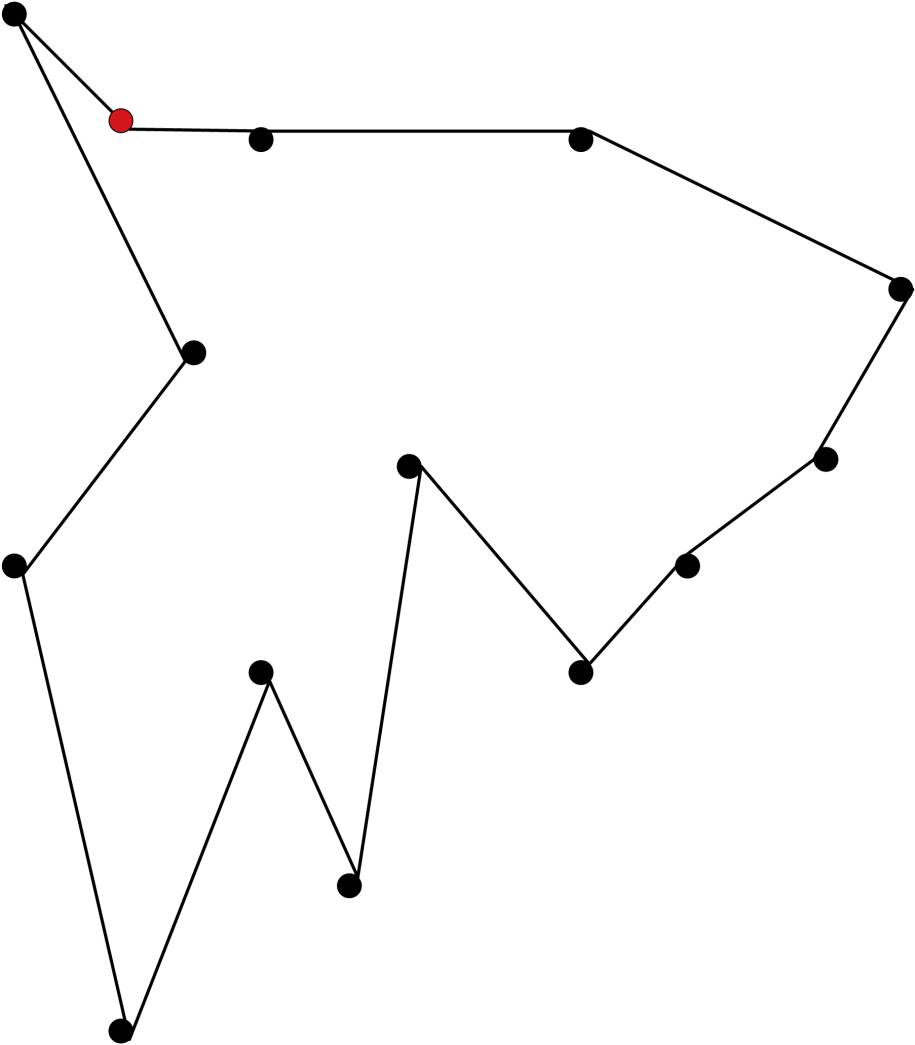
Handlungsreisendehaben ihre ganz eigenen Probleme beim Festlegen ihrer Reiserouten(Bild 5)
Bild: Google [2]
Die Reiseroute beginnt und endet am Ort mit der Nummer 0 (0 -> 9 -> 5 -> … -> 7 -> 0) und führt zu einer ermittelten Länge der Reisestrecke. Nun interessieren der Blick in den Quellcode und dazu die folgenden Fragen:
- Wie wird das Problem im Quellcode formuliert?
- Welche Klassen stehen als Hilfen zur Verfügung?
- In welcher Form werden die Koordinaten der Orte angegeben?
- Wie wird die Zielfunktion, in diesem Fall die Minimierung der Gesamtstrecke, definiert?
- Wie wird die Strecke zwischen den Orten angegeben oder errechnet?
- Wie wird die Lösung bestimmt?
Problem mit den OR-Tools lösen
Öffnen Sie dazu das vorbereitete Projekt in Visual Studio, das sich im Ordner …\examples\dotnet\Tsp befindet, und sehen Sie es sich genauer an. Ein Blick auf die Projektmappe stimmt hoffnungsvoll. Es findet sich lediglich die Referenz auf die Google OR-Tools via NuGet-Package und die Klasse TSP. Dort spielt sich der gesamte Algorithmus in der Methode Main() ab. Diese soll nun schrittweise analysiert und dabei das Vorgehen zur Definition des Problems und zur Lösung mit der Bibliothek abgeleitet werden.Werfen Sie dazu einen Blick in Listing 1. Der Quellcode ist der genannten Methode Main() entnommen und dient hier als Leitfaden durch den Algorithmus. Der einfacheren Nachvollziehbarkeit wegen sind die Zeilen des Codes für diesen Artikel nummeriert. Aus den Originalquellen wurden alle Kommentare entfernt, sodass der Algorithmus noch neun Zeilen umfasst. Die Erläuterungen im Einzelnen:Listing 1: TSP-Algorithmus aus der Beispiel-App
<span class="hljs-title">public</span> static void <span class="hljs-type">Main</span>(<span class="hljs-type">String</span>[] args) <br/>{ <br/><span class="hljs-number">1</span> <span class="hljs-type">DataModel</span> <span class="hljs-class"><span class="hljs-keyword">data</span> = new <span class="hljs-type">DataModel</span>(); </span><br/><span class="hljs-class">2 <span class="hljs-type">RoutingIndexManager</span> manager =</span><br/><span class="hljs-class"> new <span class="hljs-type">RoutingIndexManager</span>(<span class="hljs-title">data</span>.<span class="hljs-type">Locations</span>.</span><br/><span class="hljs-class"> <span class="hljs-type">GetLength(0)</span>, <span class="hljs-title">data</span>.<span class="hljs-type">VehicleNumber</span>, <span class="hljs-title">data</span>.<span class="hljs-type">Depot</span>); </span><br/><span class="hljs-class">3 <span class="hljs-type">RoutingModel</span> routing = new <span class="hljs-type">RoutingModel</span>(</span><br/><span class="hljs-class"> <span class="hljs-title">manager</span>); </span><br/><span class="hljs-class">4 var distanceCallback = new <span class="hljs-type">ManhattanDistance</span>(</span><br/><span class="hljs-class"> <span class="hljs-title">data</span>, <span class="hljs-title">manager</span>); </span><br/><span class="hljs-class">5 int transitCallbackIndex = routing.</span><br/><span class="hljs-class"> <span class="hljs-type">RegisterTransitCallback</span>(<span class="hljs-title">distanceCallback</span>.<span class="hljs-type">Call</span>); </span><br/><span class="hljs-class">6 routing.<span class="hljs-type">SetArcCostEvaluatorOfAllVehicles</span>(</span><br/><span class="hljs-class"> <span class="hljs-title">transitCallbackIndex</span>); </span><br/><span class="hljs-class">7 <span class="hljs-type">RoutingSearchParameters</span> searchParameters =</span><br/><span class="hljs-class"> operations_research_constraint_solver.</span><br/><span class="hljs-class"> <span class="hljs-type">DefaultRoutingSearchParameters</span>(); </span><br/><span class="hljs-class">8 <span class="hljs-type">Assignment</span> solution = routing.</span><br/><span class="hljs-class"> <span class="hljs-type">SolveWithParameters</span>(<span class="hljs-title">searchParameters</span>); </span><br/><span class="hljs-class">9 <span class="hljs-type">PrintSolution</span>(<span class="hljs-title">routing</span>, <span class="hljs-title">manager</span>, <span class="hljs-title">solution</span>); </span><br/><span class="hljs-class">}</span>
Schritt 1: Definition des Datenmodells (Zeile 1). Das Datenmodell enthält alle Angaben zum Problem. Es wird in einer eigenen Klasse namens DataModel definiert (Listing 2). Die Orte (Locations) werden als Array dargestellt. Jeder Ort enthält dabei eine Angabe zu den Koordinaten ([x, y]). Konkret: Der Ort mit den Koordinaten [4, 4] ist im Beispiel der Ort mit dem Index 0 im Array und damit gemäß der Problemdefinition des TSP der Start- und der Zielort (Depot). Ebenso gibt es eine Variable, welche die Anzahl der Fahrzeuge (VehicleNumber = 1) und den Ort des Depots (Depot = 0) angibt.
Listing 2: Datenmodell des TSP-Algorithmus der App
class DataModel <br/>{ <br/> public DataModel() <br/> { <br/> // Convert locations in meters using a city<br/> // block dimension of <span class="hljs-number">114</span>m x <span class="hljs-number">80</span>m. <br/> for (int i = <span class="hljs-number">0</span>; i &lt; Locations.GetLength(<span class="hljs-number">0</span>); i++) <br/> { <br/> Locations[i, <span class="hljs-number">0</span>] *= <span class="hljs-number">114</span>; <br/> Locations[i, <span class="hljs-number">1</span>] *= <span class="hljs-number">80</span>; <br/> } <br/> } <br/> public int[,] Locations = { {<span class="hljs-number">4</span>, <span class="hljs-number">4</span>}, {<span class="hljs-number">2</span>, <span class="hljs-number">0</span>},<br/> {<span class="hljs-number">8</span>, <span class="hljs-number">0</span>}, {<span class="hljs-number">0</span>, <span class="hljs-number">1</span>}, {<span class="hljs-number">1</span>, <span class="hljs-number">1</span>}, {<span class="hljs-number">5</span>, <span class="hljs-number">2</span>}, {<span class="hljs-number">7</span>, <span class="hljs-number">2</span>}, {<span class="hljs-number">3</span>, <span class="hljs-number">3</span>},<br/> {<span class="hljs-number">6</span>, <span class="hljs-number">3</span>}, {<span class="hljs-number">5</span>, <span class="hljs-number">5</span>}, {<span class="hljs-number">8</span>, <span class="hljs-number">5</span>}, {<span class="hljs-number">1</span>, <span class="hljs-number">6</span>}, {<span class="hljs-number">2</span>, <span class="hljs-number">6</span>}, {<span class="hljs-number">3</span>, <span class="hljs-number">7</span>},<br/> {<span class="hljs-number">6</span>, <span class="hljs-number">7</span>}, {<span class="hljs-number">0</span>, <span class="hljs-number">8</span>}, {<span class="hljs-number">7</span>, <span class="hljs-number">8</span>} }; <br/> public int VehicleNumber = <span class="hljs-number">1</span>; <br/> public int Depot = <span class="hljs-number">0</span>; <br/>};
Damit ist das TSP vollständig beschrieben. Ein Hinweis: Beim TSP ist die Anzahl der Fahrzeuge per Definition gleich 1. In anderen Routing-Problemen, zum Beispiel dem allgemeinen Vehicle-Routing-Problem (VRP), kann diese Anzahl auch auf einen höheren Wert festgelegt werden.Schritt 2: Definition der Klasse RoutingIndexManager (Zeile 2). Diese Klasse stammt aus den Google OR-Tools und erwartet einige Argumente zur Initialisierung: Zuerst die Anzahl der Zeilen einer Distanzmatrix für die zu besuchenden Orte; eine Distanzmatrix ist eine zweidimensionale Matrix, die Auskunft über die Entfernung zwischen zwei beliebigen Orten gibt. Da jeder Ort mit jedem anderen Ort kombiniert werden kann, entspricht die Anzahl der Zeilen und Spalten in dieser Matrix jeweils der Anzahl der Orte (siehe zum Thema auch den Kasten Die Sache mit den Entfernungen). Der nächste Parameter ist die Anzahl der Fahrzeuge und der dritte Parameter die Angabe des Depots.
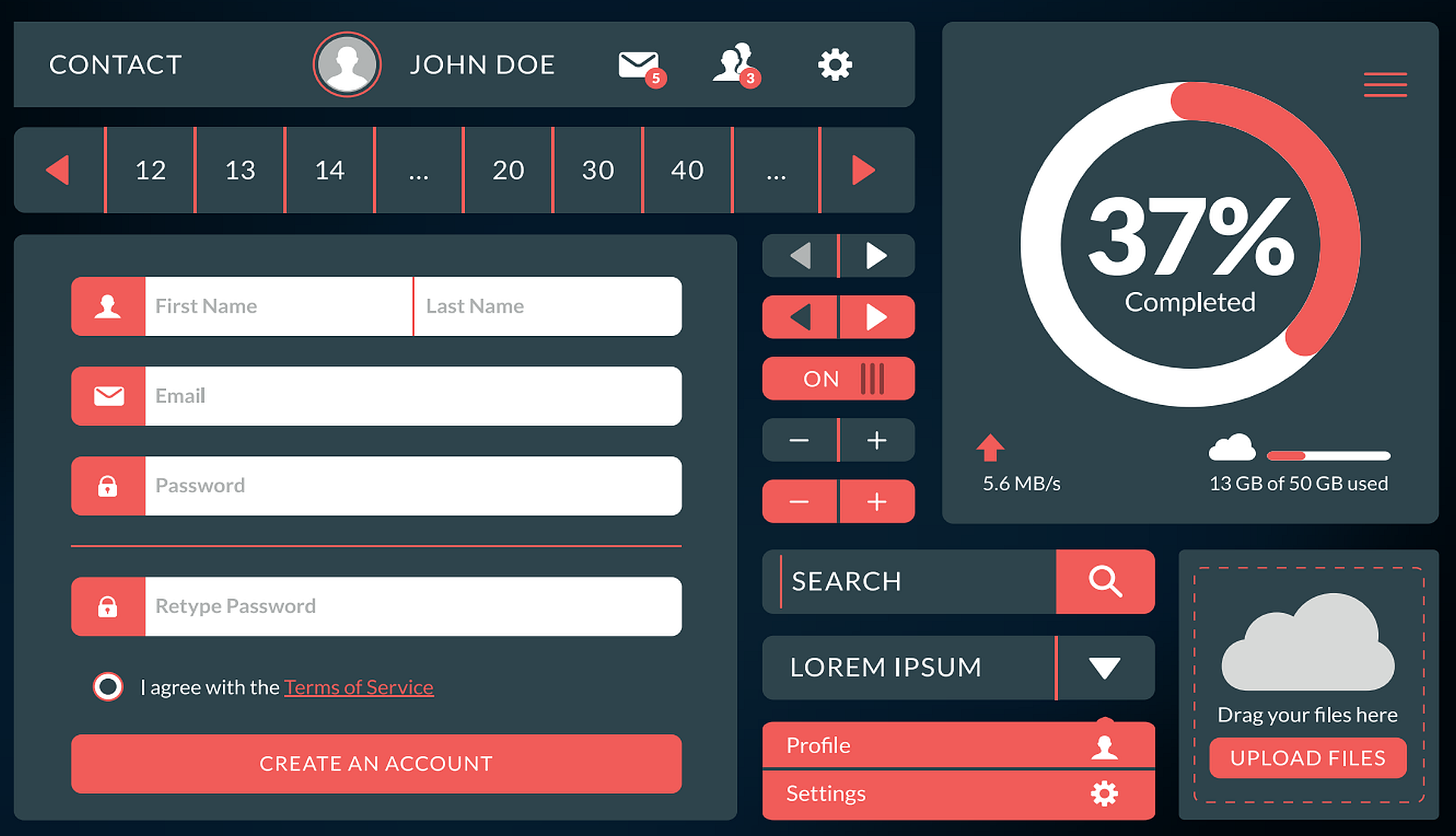
Die Sache mit den Entfernungen
Für die Bestimmung des kürzesten Wegs ist die Kenntnis der Entfernungen zwischen den Orten von entscheidender Bedeutung. Das Routing-Modell verwendet diese Angaben für die Berechnungen. Da die betreffenden Fahrzeuge theoretisch alle Orte in einer beliebigen Reihenfolge anfahren könnten, ist es notwendig, die Entfernung zwischen allen Ortskombinationen zu kennen oder diese errechnen zu können. Dazu gibt es unterschiedliche Ansätze in Theorie und Praxis, wie sich die Entfernung zwischen zwei beliebigen Orten bestimmen lässt.
Schritt 3: Definition des Routing-Modells (Zeile 3): Dieses Modell wird mit dem eben definierten RoutingIndexManager als Parameter initialisiert.Schritt 4: Eine Rückruffunktion für Entfernungen (Zeilen 4 und 5). Die Entfernung zwischen den Standorten ist die Basis für die Suche der Route. Das Lösungsverfahren der Google OR-Tools benötigt einen Verweis auf eine Methode, auf deren Basis es die Entfernung zwischen zwei beliebigen Orten bestimmen kann. Wie diese Methode konkret ausgelegt ist, also ob sie die Entfernung berechnet, die Werte aus einer Matrix ausliest oder ein webbasiertes API abfragt, spielt dabei keine Rolle. Im vorliegenden Fall definieren Sie eine Callback-Funktion für die Berechnung der Entfernung wie folgt:
<span class="hljs-keyword">var</span> distanceCallback =
<span class="hljs-keyword">new</span> <span class="hljs-type">ManhattanDistance</span>(…)
Diese Callback.-Funktion ist dann noch im Routing-Modell zu registrieren.Schritt 5: Definition des Kostenmodells (Zeile 6). Was sind die Kosten in einem Optimierungsverfahren? Das ist der numerische Wert, anhand dessen die Optimierung erfolgt. In diesem Fall ist es die ermittelte Entfernung zwischen den Standorten. Gesucht ist eine Lösung zu minimalen Kosten, das heißt mit minimaler Gesamtentfernung. Dazu definieren Sie die Callback-Funktion für die Entfernung als Kostenfunktion mit folgender Zeile:
routing<span class="hljs-selector-class">.SetArcCostEvaluatorOfAllVehicles</span>
(transitCallbackIndex)
Über die Kostenfunktion kann das Optimierungsverhalten des Algorithmus gesteuert werden.Schritt 6: Definition der Suchparameter (Zeile 7). Hier wird es spannend. Welches Lösungsverfahren (Heuristik) wird angewendet, um das Optimierungsproblem zu lösen? Im vorliegenden Fall handelt es sich um ein Tourenplanungsproblem. Hier hat die Wissenschaft eine Reihe von Lösungsverfahren entwickelt. Das Spektrum reicht über exakte Verfahren (sehr kleine Problemstellungen) über lokale Suchheuristiken bis hin zu Steuerung der lokalen Suchheuristiken durch übergeordnete Metaheuristiken. Die Google OR-Tools bieten über die Definition der Suchparameter die Möglichkeit, mit unterschiedlichen Lösungsverfahren zu experimentieren und diese dann auch einzusetzen. Es sind Algorithmen aus unterschiedlichen Kategorien implementiert. Die zugrunde liegenden Algorithmen sind kurz und knapp in der Dokumentation beschrieben [4]. Für ein weitergehendes Verständnis der Algorithmen ist dann ein umfassendes Studium der angegebenen Literatur notwendig. Die Bibliothek erlaubt es jedoch, die Algorithmen anzuwenden, ohne sie selbst implementieren zu müssen. In diesem Beispiel werden die Parameter auf den Standardeinstellungen belassen, das heißt, die Wahl des Verfahrens wird dem Algorithmus überlassen.Schritt 7: Problemlösung (Zeile 8). Die eigentliche Lösung des Problems erschöpft sich hier im Aufruf einer einzigen Methode SolveWithParameters(). Ihr werden die zuvor definierten Lösungsparameter als Argument übergeben. Hinter dem Aufruf dieser Methode verbirgt sich das gesamte Lösungsverfahren, das durch die Google OR-Tools bereitgestellt wird.Schritt 8: Ausgabe der Lösung (Zeile 9). Es wird eine eigene Methode namens PrintSolution() aufgerufen. Im Beispiel wird die Lösung als Folge der anzufahrenden Standorte und der errechneten Gesamtstrecke auf der Kommandozeile ausgegeben. In einer produktiven Anwendung werden die errechneten Ergebnisse an den Aufrufer zurückgegeben und dort weiterverarbeitet, im gewünschten Format präsentiert und gegebenenfalls grafisch aufbereitet angezeigt.Die Suche nach einer Lösung für ein Optimierungsproblem muss nicht immer zu einem Ergebnis führen. Eine Statusvariable liefert die Ergebnisse der Suche in der folgenden Form:
- 0: Problem noch nicht gelöst.
- 1: Problem erfolgreich gelöst.
- 2: Keine Lösung gefunden.
- 3: Keine Lösung vor Ablauf des Zeitintervalls gefunden.
- 5: Model beziehungsweise Parameter nicht konsistent.
Experimente mit Python
Python? Moment mal, gerade standen die Google OR-Tools für .NET (C#) im Zentrum, und nun soll es mit Python weitergehen? Genau, bei diesem Thema lohnt es sich, einen kleinen Exkurs einzulegen und über den .NET-Tellerrand hinauszuschauen. Die Entwicklung und vor allem die Konfiguration der Algorithmen erfordert es meist, minimale Anpassungen am Algorithmus vorzunehmen oder mit unterschiedlichen Parametern zu experimentieren. Dazu bietet sich die interaktive Ausführung des betreffenden Algorithmus in einem Jupyter-Notebook an.Für einen Großteil der beigefügten Beispiele gibt es vorbereitete Dateien für die Online-Version des Jupyter-Notebooks von Google, dem „Google Colaboratory“ (Bild 6), die auch online verfügbar sind [5], was einen Google-Account erfordert. Vollziehen Sie das TSP-Beispiel nach. Im Notebook müssen Sie mithilfe des ersten Codeabschnitts die Google OR-Bibliothek installieren. Danach können Sie den eigentlichen Algorithmus zum TSP interaktiv ausführen und erhalten nach kurzer Zeit das berechnete Ergebnis (Bild 7).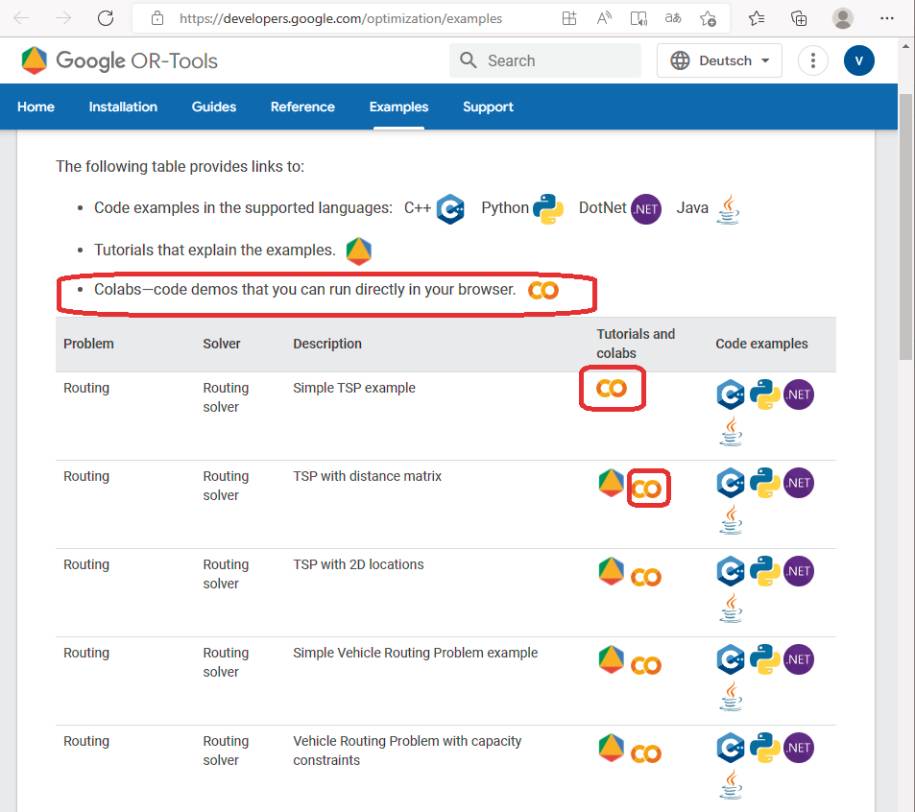
Die Algorithmender Beispiele lassen sich direkt im Jupyter-Notebook von Google öffnen(Bild 6)
Autor
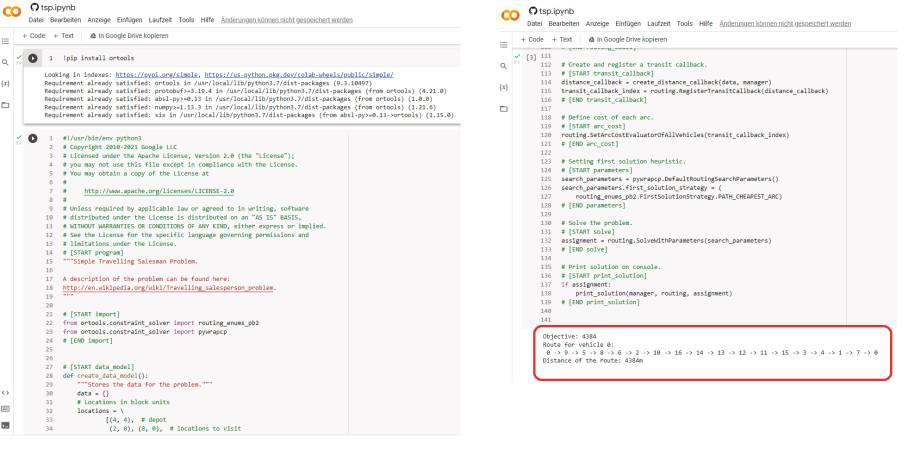
Experimentelle Ausführungder Algorithmen mit OR-Tools im Jupyter-Notebook(Bild 7)
Autor
Auf diese Weise können Sie die Lauffähigkeit des Algorithmus schneller prüfen und ihn nach Bedarf justieren. Passt alles, dann können Sie das Beispiel in .NET umsetzen und das Lösungsverfahren in eine aktive Anwendung, zum Beispiel mit grafischer Nutzeroberfläche, einbauen. Der Transfer von Python zu C# (.NET) geht dann schnell von der Hand, da die Google OR-Bibliothek für beide Programmiersprachen zur Verfügung steht.
Praxistauglichkeit
Die genannten Probleme sind nicht nur theoretischer Natur, sondern tauchen auch in der betrieblichen Praxis auf. Weist eine Frage in der Anforderungsdefinition auf Probleme in diesem Bereich hin, dann sind die Google OR-Tools mehr als einen Blick wert. Dabei wird das Problem in der Praxis selten eins zu eins mit dem Musterbeispiel übereinstimmen. In einem ersten Schritt muss das Problem genau spezifiziert und einer Problemklasse zugeordnet werden. Geht es beispielsweise um eine Frage der Routenoptimierung für Transportmittel, dann ist das Problem in Bezug auf die folgenden Größen genau zu spezifizieren:- Welches Grundproblem aus der Theorie kann als Basis herangezogen werden (TSP, VRP, Pickup- und Delivery)?
- Welche Einschränkungen und Vorgaben sind zu beachten (Zeitfenster, Ladekapazitäten der Fahrzeuge)?
- Wie viele Fahrzeuge stehen maximal zur Verfügung?
- Wie wird die Entfernung zwischen den Orten bestimmt?
- Welche Dimension hat das Problem, das heißt, wie viele Orte sind zu verplanen?
- Welche Güte der Lösung ist erforderlich?
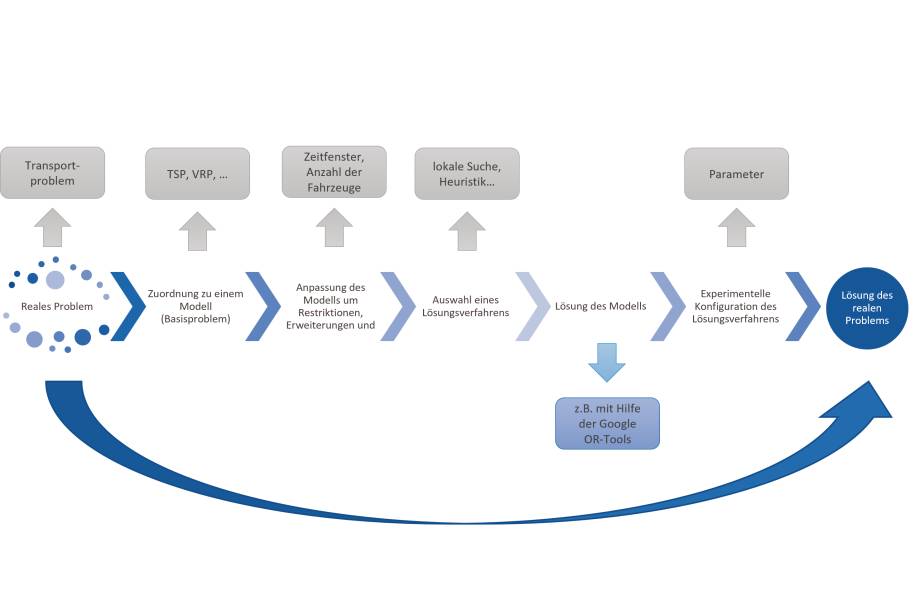
Vom realen Problemzur Lösung mithilfe der Google OR-Tools(Bild 8)
Autor
Einschränkungen
Die vorgestellten Lösungen für durchgängig komplexe Optimierungsprobleme dürfen nicht darüber hinwegtäuschen, dass nicht garantiert werden kann, dass die gefundenen Lösungen optimal sind. Beispielsweise gilt für die hier oft als Beispiel herangezogenen Vehicle-Routing-Probleme, dass diese ab einer bestimmten Anzahl von Orten nicht mehr lösbar sind und die Zeit, um alle möglichen Lösungen zu verifizieren, exponentiell mit der Größe des Problems wächst. Bei ausreichend großen Problemen kann es Jahre dauern, bis Software die optimale Lösung findet. Infolgedessen liefern auch die hier vorgestellten OR-Tools manchmal nur gute, aber nicht optimale Lösungen.Um eine bessere Lösung zu finden, sind die Suchoptionen für den Solver anzupassen. Das geht oft nur über umfassende Experimente. Die Wissenschaft hat für viele Optimierungsprobleme bereits gute Lösungsverfahren entwickelt, welche die Güte der Lösung der OR-Tools an einigen Stellen übertreffen werden.Sehr einfache Fragen, beispielsweise Rundreiseprobleme ohne Zeitfenster und Ladebeschränkungen und gleichzeitig mir nur einer begrenzten Anzahl von Standorten, lassen sich noch sehr gut mit einer Vielzahl von Algorithmen lösen, wie Studien und Experimente ergeben haben; dabei wurden standardisierte, künstlich generierte Problemdaten verarbeitet. Ab einer bestimmten Komplexität und Größe des Problems sind jedoch Transportprobleme nur noch mit einem Suchverfahren zu bearbeiten. Je nach ihrer Eignung für das spezifische Problem ermitteln diese Verfahren korrekte, brauchbare oder gute Lösungen. Optimal wird eine solche Lösung nur durch Zufall und im Einzelfall sein. Ob es so ist, wird man in der Regel auch nicht wissen.Diese Einschränkung bei der Qualität der Ergebnisse muss man immer im Hinterkopf behalten. Sie schränken jedoch die Tauglichkeit der Google OR-Bibliothek nicht ein.Fazit und Ausblick
Die Google OR-Tools sind eine interessante Sammlung von Algorithmen und Heuristiken, um Optimierungsprobleme aus den unterschiedlichsten Bereichen zu lösen. Die Probleme sind zunächst bekannte Fragen, die immer wieder in der Wissenschaft betrachtet, analysiert und gelöst werden. Es bleibt jedoch nicht bei der Theorie. Reale Probleme in der Wirtschaft lassen sich auch oft auf diese Basisfragen zurückführen. Dann können Bibliotheken eine große Hilfe bieten.Die Google OR-Tools sind auch deshalb von größerem Interesse, da sie für unterschiedliche Programmiersprachen und Entwicklungsansätze bereitstehen. Sie werden fortlaufend gepflegt und weiterentwickelt, und die vielen bereitgestellten Beispiele motivieren zum Experimentieren. Sie bieten damit eine erste Anlaufstelle für jeden, der ein konkretes eigenes Problem aus diesem Bereich lösen möchte.Fussnoten
- Elena Bochkor, Veikko Krypkzyk, Eine gute Lösung finden, Methoden des Operations Research, Teil 1, dotnetpro 8/2022, Seite 100 ff., http://www.dotnetpro.de/A2208ORTools
- Route. Schedule. Plan. Assign. Pack. Solve. – Google OR Tools, http://www.dotnetpro.de/SL2209ORTools1
- Travelling salesman problem bei Wikipedia, http://www.dotnetpro.de/SL2209ORTools2
- Distance Matrix API overview, http://www.dotnetpro.de/SL2209ORTools3
- Willkommen bei Colaboratory, http://www.dotnetpro.de/SL2209ORTools4
- Routing Options: First solution strategy, http://www.dotnetpro.de/SL2209ORTools5
